Large Language Models (LLMs) have demonstrated impressive zero-shot performance on a wide variety of NLP tasks. Recently, there has been a growing interest in applying LLMs to zero-shot text ranking. This article describes a recent paradigm that uses prompting-based approaches to directly utilize LLMs as rerankers in a multi-stage ranking pipeline.
Text Retrieval is a central component in several knowledge-intensive Natural Language Processing (NLP) applications. It refers to the task of identifying and ranking the most relevant documents, passages, sentences, or any arbitrary information snippet, in response to a given user query. The quality of text retrieval plays a crucial role in various downstream knowledge-intensive decision-making tasks, such as web search, open-domain question answering, fact verification, etc. by incorporating factual knowledge for decision-making. In large-scale industrial applications, this task is implemented as a multi-stage ranking pipeline composed of a retriever and a reranker. Popular choices for retrievers include BM25, a traditional zero-shot lexical retriever, and Contriver, an unsupervised dense retriever. {BM25, Contriver} + UPR form one of the state-of-the-art zero-shot multi-stage ranking pipeline.
Given a corpus $C = {D_1, D_2,\ldots, D_n}$ that contains a collection of documents and a query $q$, the retriever model efficiently returns a list of $k$ documents from $C$ (where $k \ll n$) that are most relevant to the query $q$ according to some metric, such as normalized Discounted Cumulative Gain (nDCG) or average precision. The reranker then improves the relevance order by further reranking the list of $k$ candidates in the order of relevance according to either the same or a different metric. The reranker is usually a more effective but computationally more expensive model compared to the retriever.
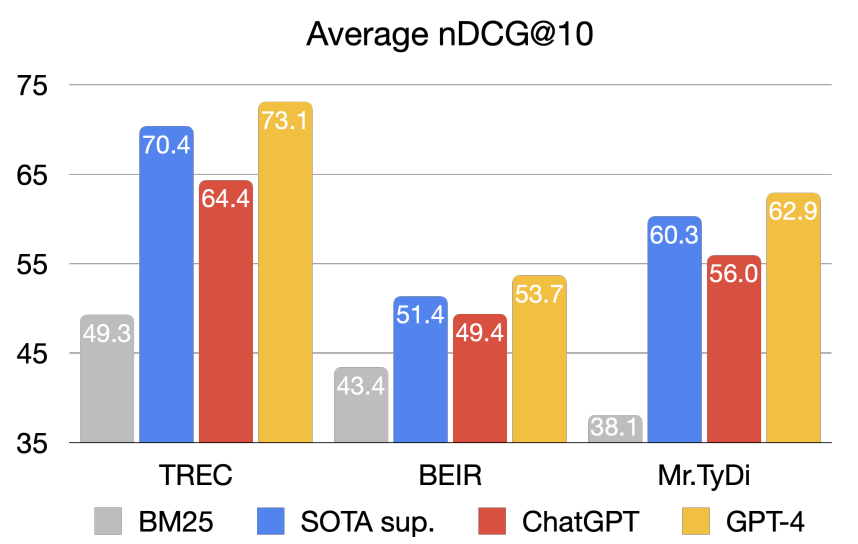
Large Language Models (LLMs) have demonstrated impressive performance on a wide range of NLP tasks. LLM-based text retrievers excel in contextualizing user queries and documents in natural language, often handling long-form or even conversational inputs. These LLMs have also been adapted for zero-shot and few-shot document ranking tasks through various prompting strategies. Sun et al. showed that GPT-4 with zero-shot prompting surpassed supervised systems on nearly all datasets and outperformed previous state-of-the-art models by an average nDCG improvement of 2.7, 2.3, and 2.7 on TREC, BEIR, and My.TyDi, respectively. Among the proprietary LLMs, GPT-4 outperformed Cohere’s Rerank, Anthropic’s Claude-2, and Google’s BARD.
Recent works, such as InPars, Promptagator, HyDE, use LLMs as auxiliary tools to generate synthetic queries or documents to augment the training data for retrievers or rerankers. Interested readers can refer to the article linked below to read more about these unsupervised methods. The focus of this article instead will be on the methods that directly use LLMs as rerankers in the multi-stage pipeline.
This article reviews some of the recent proposals from the research community to boost text retrieval and ranking tasks using LLMs.
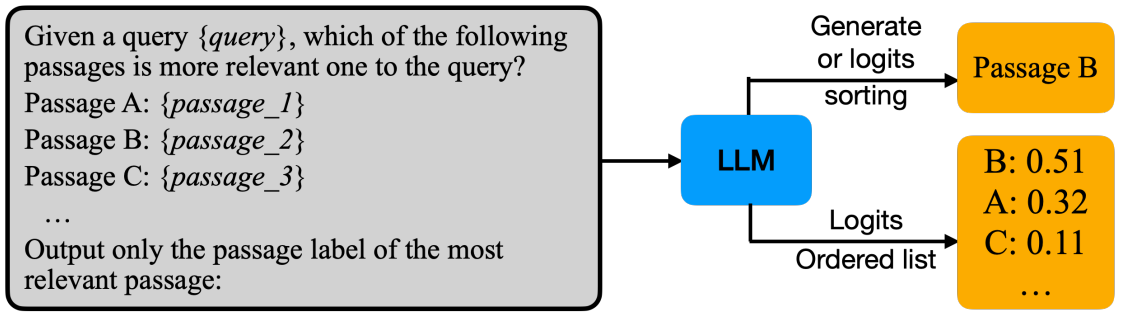
Based on the type of instruction employed, the ranking strategies for utilizing LLMs in ranking tasks can be broadly categorized into three main approaches: Pointwise, Pairwise, and Listwise methods. Given the user query and candidate documents as input, these methods employ different prompting methodologies to instruct the LLM to output a relevance estimation for each candidate document.
Given a query $q$ and a set of candidate items $D={d_1, d_2, \ldots, d_n}$, the objective is to determine the ranking of these candidates, represented as $R={r_1, r_2, \ldots, r_n}$. Here, $r_i \in {1,2,\ldots,n}$ denotes the rank of the candidate $d_{i}$. For example, $r_i=3$, means that the document $d_i$ is ranked third among the $n$ candidates. A ranking model $f(.)$ assigns scores to the candidates based on their relevance to the query: $s_{i}=f(q,d_i)$, and the candidates are then ranked according to these relevance scores: $r_i= arg sort_i(s_1,s_2,\ldots,s_n)$.
In the pointwise ranking method, the reranker takes both the query and a candidate document to directly generate a relevance score. These independent scores assigned to each document $d_i$ are then used to reorder the candidate set $D$. The relevance score is typically calculated based on how likely the document is relevant to the query or how likely the query can be generated from the document.
This method can be further classified into two popular approaches based on how the ranking score is calculated.

ln instructional relevance generation approaches, like Liang et al., the LLMs are generally prompted to output either “Yes” or “No” to determine the relevance of the candidates to a given query. The generation probability is then converted to the relevance score:
$$ s_i = \begin{cases}
1 + f(\text{Yes} | I_{\text{RG}}(q,d_i)), & \text{if output Yes} \
1 – f(\text{No} | I_{\text{RG}}(q,d_i)), & \text{if output No}
\end{cases} $$
Here $f(.)$ represents the large language model, and $I_{RG}$ denotes the relevance generation instruction that converts the input $q$ and $d_i$ into the text-based prompt.
Query generation approaches, like Sachan et al., use LLMs to generate a query based on the document and measure the probability of generating the actual query.
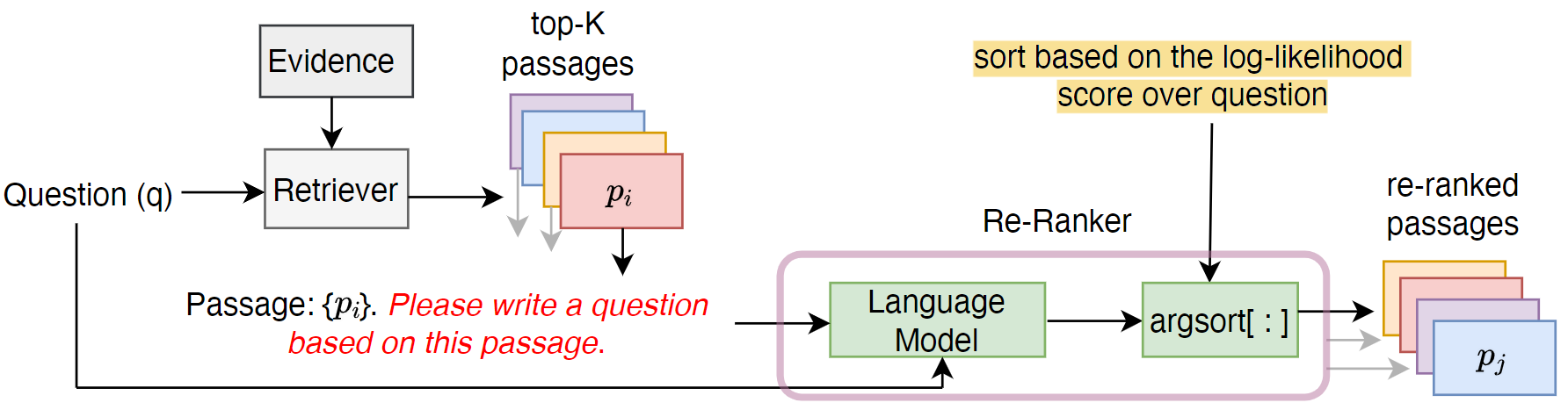
An example of this approach is the Unsupervised Passage Re-ranking (UPR) by Sachan et al. UPR follows a zero-shot document reranking approach by applying an off-the-shelf pre-trained language model (PLM). It appends a natural language instruction “Please write a question based on this passage” to the document $d_i$ (or “passage”) tokens and computes the likelihood of query (or “question”) generation conditioned on the passage:
$$ \log p(q | d_i) = \frac{1}{|q|} \sum_{t} \log p(d_t | q_{<t}, d_i; \Theta) $$
where $\Theta$ denotes the PLM parameters, and $|q|$ denotes the number of question tokens. The candidate set of documents is then sorted based on $\log p(q | z)$. UPR codebase including data and checkpoints is available on GitHub.
In pairwise ranking strategy, a pair of candidate items ($d_i, d_j$) along with the user query ($q$) serve as prompts to guide the LLMs to determine which document is the most relevant to the given query.
$$ c_{i,j} = \begin{cases}
1, & \text{if } f(I_{\text{PRP}}(q, d_i, d_j)) = i \
0, & \text{if } f(I_{\text{PRP}}(q, d_i, d_j)) = j \
0.5, & \text{else}
\end{cases} $$
Here, $c_{i,j}$ denotes the choice of LLM $f(.)$, and $I_{PRP}$ is a specific pairwise comparison instruction employed to instruct the LLM. This approach usually consults the LLM twice (with $I_{PRP}(q, d_i, d_j)$ and $I_{PRP}(q, d_j, d_i)$) for every pair $d_i$ and $d_j$ because LLMs exhibit sensitivity to the order of the text in the prompt.
Handling inconsistent outcomes
If both $I_{PRP}(q, d_i, d_j)$ and $I_{PRP}(q, d_j, d_i)$ promptings make consistent decisions, we have local ordering $r_i$ > $r_j$ or $r_i$ < $r_j$, else we assume $r_i = r_j$ (each document gets half a point).
Subsequently, to compute the relevance score of the $i$-th candidate $d_i$, this method compares $d_i$ against all other candidates in the set $D$ to aggregate the final relevance score as: $s_i = \sum_{j \neq i} c_{i,j} + (1 – c_{j,i})$ . For ties in the aggregated scores, the Pairwise ranking method has been proven to be more effective than pointwise and listwise methods, but it is also inefficient and hence unsuitable for inference in large-scale industrial systems. Recent studies have proposed a few methods to reduce some of its time complexity.
Pairwise reranking is often quite effective, but this strategy has a high runtime overhead of transformer inferences. For a set of $k$ documents to be ranked, preferences for all $k^2-k$ comparison pairs, excluding self-comparison, are to be aggregated. Though these calls to LLMs can be parallelized, the $O(k^2)$ calls can be prohibitive in terms of cost. However, some of the comparisons may be redundant in that they can be predicted from those of other comparisons. A theoretical lower bound on the runtime complexity is $O(k \log{k})$ if the estimated comparisons were consistent and transitive. Some researchers have suggested improving the pairwise reranking efficiency without a significant loss of effectiveness by sampling from all pairs.
-
Gienapp et al. studied three sampling methods with pointwise monoT5 and pairwise duoT5 models.
- Global Random Sampling: For each of the top-$k$ documents, a fraction of $k-1$ documents is randomly chosen for the comparison set.
- Neighborhood Window Sampling: A sliding window of size $m \le k-1$ is moved over the top-$k$ documents and the $m$ documents are sampled for comparison. The window “wraps around” when it has less than $m$ documents.
- Skip-Window Sampling: While the neighborhood window sampling method samples from a “local” neighborhood, the skip-window sampling enabled more “global” comparisons by incorporating a skip size $s$. This method is the same as neighborhood window sampling when $s=1$.
The study showed that the best combination (Skip-Window Sampling with greedy aggregation) allows for an order of magnitude fewer comparisons at an acceptable loss of retrieval effectiveness, while competitive effectiveness was achieved with about one-third of comparisons. All code and data underlying this experiment are available on GitHub.
-
Mikhailiuk et al. proposed ASAP (Active Sampling for Pairwise comparisons) sampling strategy for collecting pairwise comparison data. The authors share propose a taxonomy for existing methods and divide them into four groups, based on the type of approach: passive, soring, information-gain, and matchmaking. Their ASAP is a fully Bayesian algorithm that computes the posterior distribution of scores variable $r$ that would arise from each possible pairwise outcome in the next comparison and then uses this to choose the next comparison based on a criterion of maximum information gain. It also allows for a batch sampling mode by sampling the pairs from a minimum spanning tree. ASAP codebase is available on GitHub.
-
In pairwise ranking prompting (PRP) Qin et al. proposed two methods to improve pairwise ranking efficiency. They use Heapsort with pairwise preferences from LLMs as the comparator for the sorting algorithm. They also utilize a sliding window approach, in which a window starts from the bottom of the list, compares and swaps document pairs with a stride of 1. One sliding window pass is similar to one pass in the Bubblesort algorithm and one pass only requires $O(k)$ time complexity.
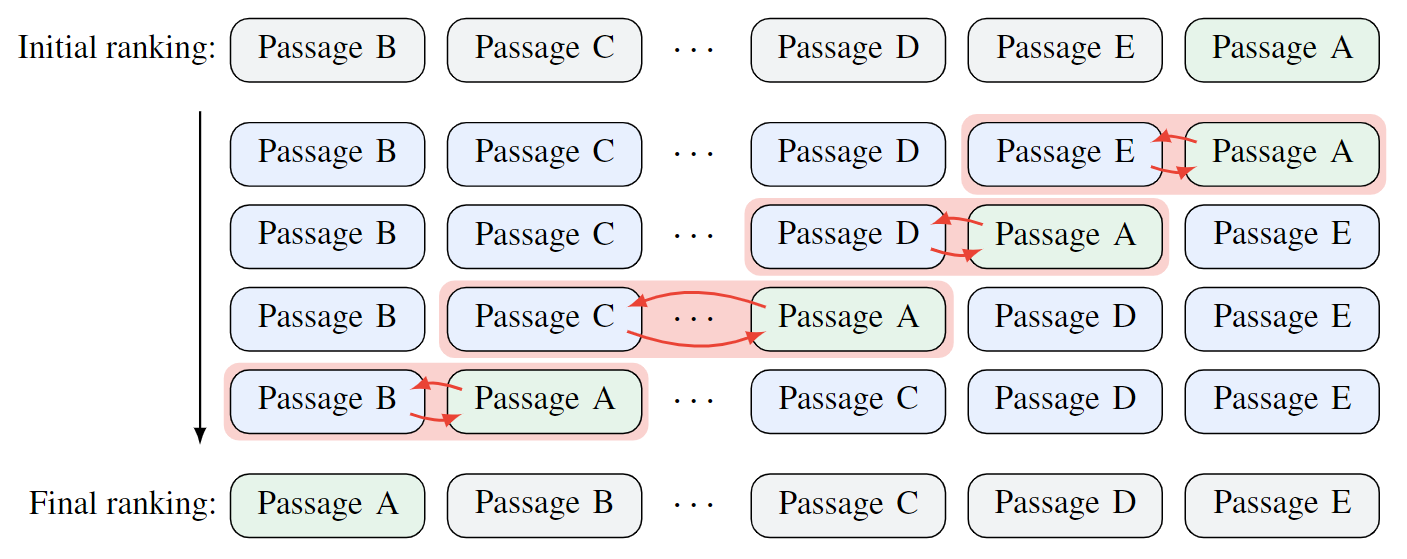
One pass of PRP’s sliding window approach. k such passes are performed to get top-k ranking results. Their experiments show that the PRP-based FLAN UL2 model with 20B parameters matches and often outperforms blackbox commercial GPT-4 which has a 50x (estimated) model size.
-
Zhuang et al. proposed a Setwise prompting technique that improves the efficiency of pairwise models. Their work is based on a simple realization that the sorting algorithm employed by pairwise approaches, like PRP, can be accelerated by comparing multiple documents at each step, as opposed to just a pair. Their experiments show that incorporating the setwise prompting significantly improves the efficiency of both pairwise and listwise approaches, while also enhancing the robustness to initial document ordering. The authors also share a systematic evaluation of all existing LLM-based zero-shot approaches under consistent experimental conditions.
With scoring-API-based pairwise renraking, assuming a set of $k$ candidate documents to be reranked, preference probabilities for all $k^2-k$ document pairs (excluding self-comparison) are aggregated using rank aggregation strategies. Static aggregation methods assume that the required pairwise comparisons are done before the aggregation starts, while the dynamic aggregation methods decide which documents to compare next based on all previous comparisons. Several approaches are known to work well in practice. Some of these approaches are mentioned below:
- Sorting via KwikSort: Kwiksort is an extension of the QuickSort algorithm for data with preferences. It works recursively by randomly picking a pivot document and placing the documents ranked lower or higher than the pivot in separate subsets. This method assumes that the comparisons are consistent and has $O(k \log{k})$ as the expected number of comparisons.
- Additive Aggregation: Pradeep et al. proposed an approach where the rank of a document is indicated by the sum of the document’s comparison probabilities (potentially transforming the probabilities before summation).
- Regression-based Aggregation: Using the Bradley-Terry model, the latent scores for documents can be learned using maximum likelihood estimation such that they optimally correspond to a given set of pairwise comparisons.
- Greedy Aggregation: In greedy aggregation methods, a heuristic iteratively selects and removes the best document from a given set and then proceeds with the rest.
- Graph-based Aggregation: Comparison can also be interpreted as directed weighted edges between the document nodes. A measure of graph centrality, such as PageRank, can then be used to derive a ranking score.
The listwise paradigm generalizes the pairwise paradigm. In the listwise ranking strategy, a set of candidate documents is fed to the LLM. This means that the model can attend to all the candidate documents simultaneously while reranking. Each document is identified by a unique identifier like [1], [2], etc. The LLM is then instructed to generate a ranked permutation of these documents, such as [2] > [3] > [1]. $Perm = f(I_{LIST}(q,d_1,d_2,\ldots,d_n))$ . By framing its goal as text generation, this approach fuses well with the existing techniques based on generative models.
Some work also refer to this approach as the Instructional Permutation Generation approach as it instructs the LLM to directly output the permutations of a group of passages. LLMs that are used as rerankers in a multi-stage pipeline, with prompt engineering being the primary means to accomplish the listwise reranking tasks, have also been referred to as the “prompt decoders”. Listwise approaches can be inefficient because of the substantial number of required tokens in the output as each additional token generated by LLM requires an extra inference step.
The relevance score for each candidate is simply defined as the reciprocal of its rank $s_i = \frac{1}{r_i}$. So the generated permutation can be readily transformed into ranking results $R$.
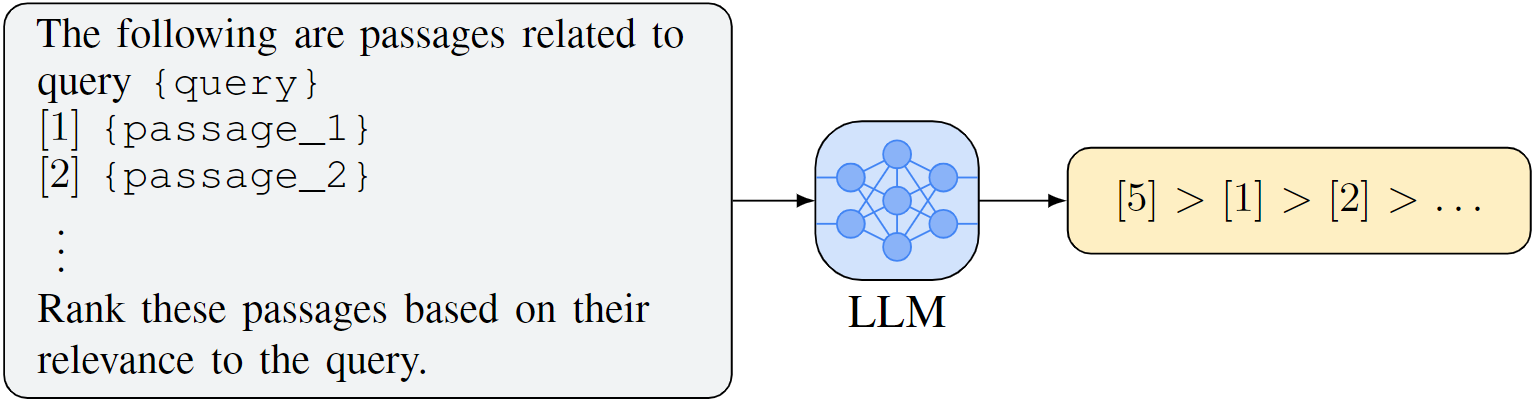
Due to the token limit on input context, LLMs can only rank a limited number of passages using the listwise ranking approach. To overcome this, a sliding window strategy is employed to allow the LLM to rank an arbitrary number of passages.
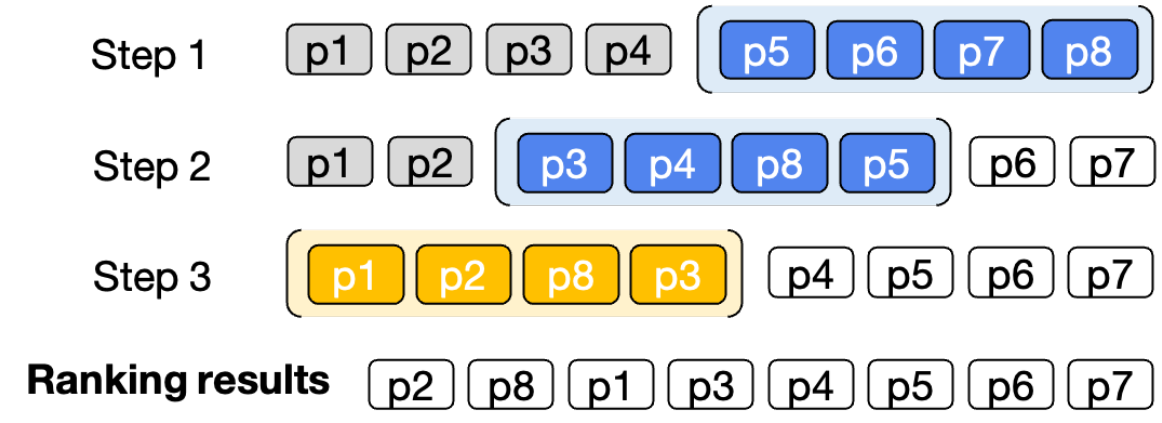
The above figure shows an example of reranking 8 passages using a sliding window of size 4, and a step size of 2, being applied in back-to-first order. The first two windows are shown using blue color and the last window is shown in yellow color. The first two passages in the previous window will participate in the reranking of the next window.
Formally, for reranking $M$ passages, we define two hyperparameters: window size $(w)$ and step size $(s)$. LLM is used first to rank the candidates from $(M-w)$ to $M-th$ passage, and then we slide the window in step size of $s$. Then we rerank the passages in $(M-w-s)$ to $(M-s)$ range. In each step, the top $(w-s)$ candidates are preserved and form the next sliding window together with the next $s$ documents. We repeat this process of ranking $w$ passages while sliding the window forward with the step size $s$ until all the passages have been reranked.
Recent studies have shown that the top-ranked passages by listwise rerankers come from a wide range of positions, compared to the pointwise methods. While pairwise approaches may elevate a poorly ranked relevant document to a high position, they usually fail to reorder multiple items effectively. On the other hand, listwise methods, with large context windows, excel at concurrently promoting several poorly ranked documents into higher position .
Listwise-ranking strategy is highly efficient, but using off-the-shelf models it has mostly been effective with some powerful LLMs, such as Claude and GPT4 as the smaller models seem to lack the capability to effectively reorder a list of input documents. This strategy also relies heavily on intricate prompt engineering and has been shown to generate malformed outputs, such as:
- Incorrect output format: LLM outputs may not follow the requested format
- Repetition: output response may contain repeated document IDs
- Missing: some document IDs might be missing in the LLM response
Pradeep et al. used RankGPT-3.5 as the teacher model to generate a ranked list to train their student model. They found that about 12% of the outputs were malformed and had to be excluded from the training set for the student model.
Among the three approaches described above, the pairwise method is the most efficient as it computes the relevance score for each document for a given query only once and can be parallelized. However, it may not be a highly effective approach as it considers each document independently without information about each other and requires the model to yield a calibrated pointwise score. In contrast, the pairwise paradigm solves the calibration issue by considering one-to-one pairwise comparisons. However, LLM inference on all document pairs can be computationally expensive. The Listwise ranking is more efficient than the pairwise approach, but its effectiveness is limited to closed-source LLMs like GPT-4, as it has been shown to perform poorly on smaller, open-source models. Listwise methods also struggle with including a large candidate set of documents into the prompt due to the prompt length constraints. So most practical implementations use a sliding-window (size $k$) method (more on this later).
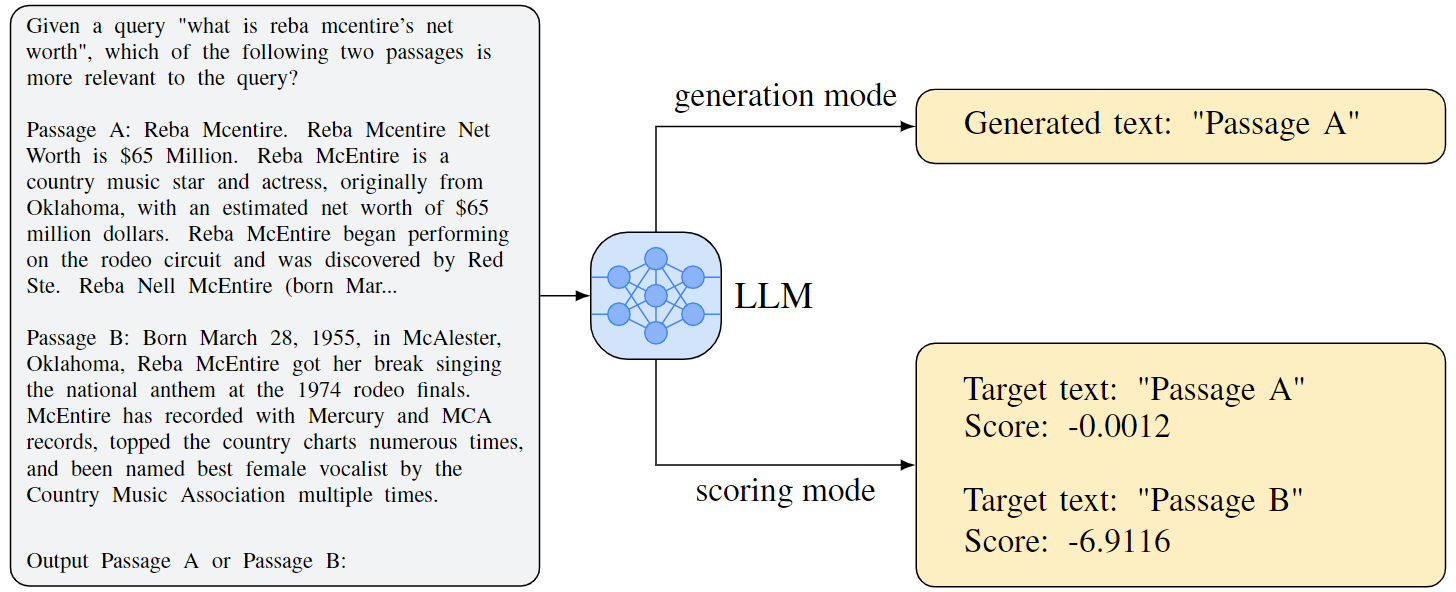
With LLM prompting, there are two popular modes of ranking documents: generation and scoring/likelihood. For pointwise ranking with the generation approach, LLM is asked a “yes/no” question about whether the candidate document is relevant to the query. The normalized likelihood of generating a “yes” response for each of the documents is used as the relevance score for reranking the candidate documents. Whereas in the scoring approach, a query likelihood method reranks the documents based on the likelihood of generating the actual query.
Closed source LLMs
Note that both of these methods require access to the output logits of the LLM to be able to compute the likelihood scores. Hence it is not possible to use closed-sourced LLMs, like GPT-4, to implement these approaches when the corresponding APIs do not expose the logit values.
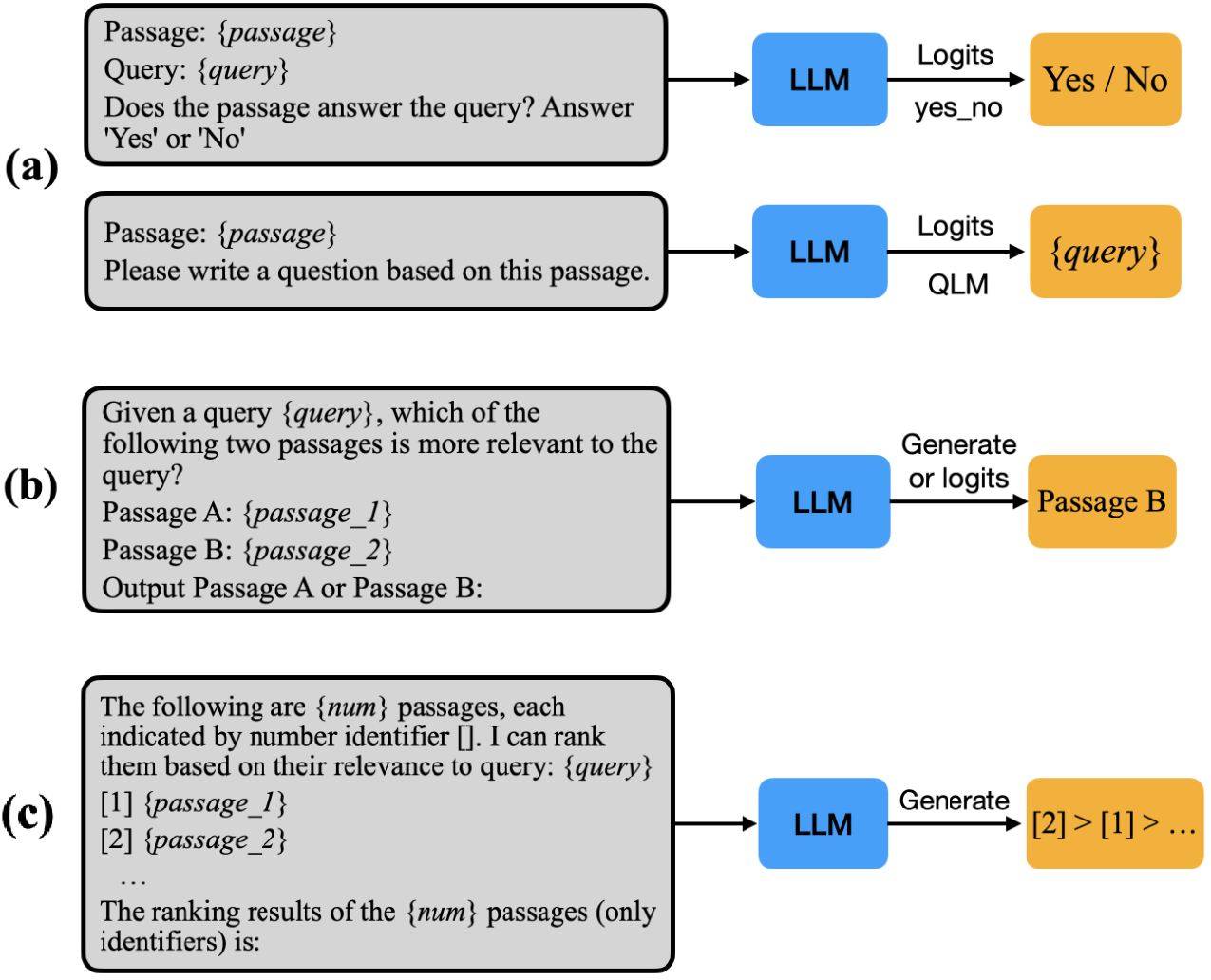
Pairwise ranking naturally supports both generation and scoring LLM APIs. Listwise ranking approaches follow the more efficient permutation generation process for directly generating the ranked list of document identifiers without producing any intermediate relevance score.
| Approach | Complexity | Generation API | Scoring API | Require Calibration | Batch Inference |
|---|---|---|---|---|---|
| Pointwise | $O(n)$ | No | Yes | Yes | Yes |
| Pairwise – all pairs | $O(n^2 – n)$ | Yes | Yes | No | Yes |
| Pairwise – heasort | $O(n \log_{2}{n})$ | Yes | Yes | No | No |
| Listwise | $O(k*n)$ | Yes | No | No | Yes |
The emergence of LLMs has brought a paradigm shift in natural language processing. And, there has been a growing interest in harnessing LLM powers for text ranking. Most existing approaches exploit LLMs as an auxiliary tool for content generation (e.g. query or passage). This article reviewed recent research direction that directly prompts LLMs to perform unsupervised ranking using pointwise, pairwise, or listwise techniques. In the next article, we will take a closer look at some of the challenges associated with this theme and strategies toward more effective and efficient LLM-based reranking. We will also explore the latest efforts to train ranking-aware LLMs.