Quicksort written in Python only using lambdas!

GitHub: https://github.com/lucasoshiro/lambdasort

Lambda calculus

Python, just like many other programming languages, supports high-order
functions and anonymous functions. This means, basically, that we can
do this:

# anonymous function (lambda). This is equivaltent to sqrt:
lambda n: n ** 0.5

# function that takes another function as parameter
def apply_func(func, parameter):
    return func(parameter)

# function that returns another function. in this case, this is a mutiplier factory
def multiplier_factory(n):
    return lambda x: n * x

Right. This way, functions are values that can be created and returned by
other functions.

What if we write a code that the type of every value is a function? For example:

t = lambda a: lambda b: a
f = lambda a: lambda b: b
x = (lambda a: lambda b: a(b)(f))(t)(f)

At first look it seems to be useless. However, believe it or not (spoiler: this
will be explained further), that is a boolean and of True and False!

This is the famous lambda calculus. It only has functions that get
functions as parameters and return other functions. For us, that is enough, but
if you want to read more about it, I really suggest you
this article on Wikipedia.

Even though it seems to be insufficient to do anything, actually lambda calculus
can solve any problem that can be solved with an algorithm, as it is
Turing-complete! Alan Turing
itself has proven it!

The excellent Programming with Nothing
by Tom Stuart shows how to write a fizzbuzz using lambda calculus in Ruby.
When I read it the first time I wanted to do something similar to it, so I made
this: A QUICKSORT IN LAMBDA CALCULUS.

I will tell you all the steps of how I did that!

The beginning: a normal quicksort in Python

The first step was to write a quicksort in Python, but with a difference
compared to the traditional quicksort: it doesn’t change the original list,
instead, it returns a new list, just like the sorted in Python:

def car(A):
    return A[0]

def cdr(A):
    return A[1:]

def cons(A, x):
    return [x] + A

def concat(A, B):
    return A + B

def quicksort(A):
    if len(A) <= 1: return A
    L, R = partition(A)
    p = car(R)
    L = quicksort(L)
    R = quicksort(cdr(R))
    return concat(L, concat([p], R))

def partition(A):
    p = car(A)

    L, R = [], []

    for x in cdr(A):
        if x < p:
            L, R = cons(x, L), R
        else:
            L, R = L, cons(x, R)

    L, R = L, cons(p, R)

    return L, R

Take a look in the use of the functions car, cdr and cons. I followed the
Lisp nomenclature for those functions. They will be further
implemented the same way as some Lisp dialects, so I tried to be closer to them
in how lists work instead of the usual in Python:

• The car function returns the first element
• The cdr function returns a list with the rest of the elements. In other
  words, all the elements except the first
• By now, I also implemented cons as a function that returns a new list that
  looks the same as the provided but appending a new element to its
  beginning, but cons is more than that (I’ll discuss it later)
• The concat function concatenates two lists.

The rest is only a standard quicksort:

• The partition function splits a list in two, the left one being a list
  that all of its elements are lesser than the first element of the right one
  (the pivot), and the right one being a list that all elements are greater or
  equal to the pivot.

• The quicksort function calls partition to split the list that we want to
  sort into two and sorts each one using quicksort itself, recursively,
  being the base of the recursions lists with length lesser or equal to 1.

As for the weird constructions L, R = ..., by now it is useless to do those
parallel attributions, but this will be helpful in the future.

You can see it here.

Redefining types

As the idea is to rewrite quicksort using only lambdas, we need to somehow represent
data using only functions. The types here are:

• integers (the values in the list that we want to sort)
• lists
• pairs (used by the functions that return more than one value)
• booleans (used by the verifications)

Luckily, the creator of lambda calculus, Alonzo Church has also shown us how
to do that. There’s an article about it
on Wikipedia.

Booleans

Let’s start by the easier ones, booleans:

#boolean constants
LAMBDA_TRUE = lambda a: lambda b: a
LAMBDA_FALSE = lambda a: lambda b: b

#boolean opearations
LAMBDA_OR = lambda a: lambda b: a(LAMBDA_TRUE)(b)
LAMBDA_AND = lambda a: lambda b: a(b)(LAMBDA_FALSE)
LAMBDA_NOT = lambda a: a(LAMBDA_FALSE)(LAMBDA_TRUE)

Yeah, true is only a function that takes two arguments and returns the
first one, and false is a function that takes two arguments and returns
the second one.

I know that you’re thinking: “it should be lambda a, b: a and lambda a, b:
b, why there are two lambdas?”. This is because in the definition of lambda
calculus, functions can only take one argument. Contrary to that definition,
in Python lambda can take zero or more arguments, but here I’m restricting
myself to only use functions that take only one argument in order to stick to
the definition. This way, what would be written as lambda a1, a2, a3, ..., an:
will be written as lambda a1: lambda a2: lambda a3: ... lambda an:. When
calling the function, we use (a1)(a2)(a3)...(an) instead of (a1, a2,
a3, ..., an). The name of that conversion is
currying, named after Haskell
Curry. An example of language that natively uses currying to handle function is
Haskell (you don’t say!).

After that, I implemented the tree basic boolean operations:

• not: takes a Church boolean, and calls it using as parameters false and
  true. If the boolean is true, it returns the first argument (false);
  if it is false, then it returns the second argument (true).

• or: takes two Church booleans, calls the first one passing as arguments
  true and the second boolean. If the first argument of or is true, then
  it returns its first argument (true); if it is false, then it returns
  its second argument (the second argument of or).

• and: much like or. Try to simulate it mentally 😉

We can also define an if:

if

LAMBDA_IF = lambda c: lambda t: lambda e: c(t)(e)

In if, cis the condition; t is the “then” block, what happens when the
condition is true, and e is the “else” block, what happens when the
condition is false.

This way, if is closer to an if-expression in Python (or ternary operator)
than a control flow if:

use_5 = LAMBDA_TRUE
dont_use_5 = LAMBDA_FALSE

a = LAMBDA_IF(use_5)(5)(0) # a = 5
b = LAMBDA_IF(dont_use_5)(5)(0) # a = 0

Conversion

I also defined two functions to convert Church booleans to Python booleans
(l2b) and vice-versa (b2l):

#boolean conversion
def l2b(l):
    return l(True)(False)

def b2l(b):
    return LAMBDA_TRUE if b else LAMBDA_FALSE

Mental exercise: simulate them!

You can see it here

Integers

Church numerals are defined as:

LAMBDA_ZERO = lambda p: lambda x: x
LAMBDA_ONE = lambda p: lambda x: p(x)
LAMBDA_TWO = lambda p: lambda x: p(p(x))
# etc

This is, all the integers are functions that take two arguments p and x
this way:

• 0 is a function that returns x (just like false)
• 1 is a function that returns p(x)
• 2 is a function that returns p(p(x))

and so on. However, we can represent negative numbers using this encoding.

Increment and decrement

Increment is easy to define, it is a function that adds another layer of p(...):

LAMBDA_INCREMENT = lambda l: lambda p: lambda x: p(l(p)(x))

But decrement is far harder. Explaining it takes some time, and
understanding it is not useful for us right now. If you really want to know how
it works, try it by yourself. If you don’t care, just trust me Church that
it works:

LAMBDA_DECREMENT = lambda n: lambda f: lambda x: n(lambda g: lambda h: h(g(f)))(lambda y: x)(lambda y: y)

If you tried to simulate it by yourself, you probably tried to figure out what
happens if you decrement zero. And you found that the decrement of zero is
zero here. Sadly this is a limitation, and we’ll need to remember it soon in
the future.

Add and subtraction

Ok, we have increment and decrement. If we increment n times a number m,
then we’ll have m + n, and if we decrement n times we’ll have m - n.

We can define add and subtraction this way:

LAMBDA_ADD = lambda m: lambda n: n(LAMBDA_INCREMENT)(m)
LAMBDA_SUB = lambda m: lambda n: n(LAMBDA_DECREMENT)(m)

Note that increment and decrement will passed as the p argument of the number
n and m will be the x argument. In other words, m will be incremented or
decremented the same amount of times than the number of calls that p has
in n, this is, n times. Very, very beautiful.

Even so, a consequence of the decrement of zero being zero here is that n - m
will always be zero if m > n.

Multiplication and division are also possible, but they won’t be useful for this
quicksort.

Comparisons

The integer operations that will actually be useful for implementing quicksort
are the comparisons. Let’s start by defining the function that tells if a
Church number is or not zero (mental exercise: why does this work?):

LAMBDA_EQZ = lambda n: n(lambda x: LAMBDA_FALSE)(LAMBDA_TRUE)

Using only the operation of equals zero, combined with boolean and
arithmetic operations we can define the others:

• m <= n: (m - n) == 0 (remember: m - n = 0 if n > m)
• m == n: (m <= n) and (n <= m)
• n < m: (m <= n) and not (m == n)

Or, in Python / lambda calculus:

LAMBDA_LEQ = lambda m: lambda n: LAMBDA_EQZ(LAMBDA_SUB(m)(n))
LAMBDA_EQ = lambda m: lambda n: LAMBDA_AND(LAMBDA_LEQ(m)(n))(LAMBDA_LEQ(n)(m))
LAMBDA_LESS = lambda m: lambda n: LAMBDA_AND(LAMBDA_LEQ(m)(n))(LAMBDA_NOT(LAMBDA_EQ(m)(n)))

Conversion

If we want to convert a Church number to a Python integer we’ll only need to
pass the increment function as the first argument (p) and 0 as the second:

def l2i(l):
    return l(lambda x: x + 1)(0)

We can do the inverse: we can increment several times the Church zero until
we reach the number:

def i2l(i):
    l = LAMBDA_ZERO
    for j in range(0, i):
        l = LAMBDA_INCREMENT(l)

    return l

We can also define functions to convert Python integer lists into Church number
lists and vice-versa:

def llist2pylist(L):
    return list(map(l2i, L))

def pylist2llist(L):
    return list(map(i2l, L))

Using Church numbers

As we can convert Python integer lists into Church number lists and vice-versa
and we can compare Church numbers, we can apply the first change to Quicksort:

def quicksort(A):
    if len(A) <= 1: return A
    L, R = partition_wrapper(A)
    p = car(R)
    L = quicksort(L)
    R = quicksort(cdr(R))
    return concat(L, concat([p], R))

def partition_wrapper(A):
    B = pylist2llist(A)
    L, R = partition(B)
    return llist2pylist(L), llist2pylist(R)

def partition(A):
    p = car(A)

    L, R = [], []

    for x in cdr(A):
        if l2b(LAMBDA_LESS(x)(p)):
            L, R = cons(x, L), R
        else:
            L, R = L, cons(x, R)
    L, R = L, cons(p, R)

    return L, R

The partition function now operates over Church number lists. In order to
do that, we replaced x < p by LAMBDA_LESS(x)(p), that returns a Church
boolean instead of True and False. I needed to use l2b to convert the
Church boolean to a Python boolean so we can keep the compatibility with if.

The function partition_wrapper adapts the new partition in a way that it
takes Python integers, but partitioning using the new partition function.

In the following sections I will make several substitutions of types, functions
and operators by functions in lambda calculus, just like I did so far. I’ll try
to change only what is relevant for each step, using the conversion functions if
necessary.

You can see it here.

Pairs and lists

Our basic data structure is the pair. The pair is really a pair of values,
just like a Python tuple of size 2. In Church encoding, a pair and its basic
operations are defined like this:

LAMBDA_CONS = lambda a: lambda b: lambda l: l(a)(b)
LAMBDA_CAR = lambda p: p(lambda a: lambda b: a)
LAMBDA_CDR = lambda p: p(lambda a: lambda b: b)

The first function, LAMBDA_CONS, defines the pair. Note that, when passing two
values as its arguments (e. g. LAMBDA_CONS(15)(20)), it will return a function
that takes an argument l and returns the l call using the pair elements
as arguments (in our example, l(15)(20)). That is: LAMBDA_CONS(15)(20) =
lambda l: l(15)(20). In Python and other languages that supports first-class
functions, those two values are stored in a
closure, and
we can even get them this way:

l = LAMBDA_CONS(15)(20)
a, b = (x.cell_contents for x in l.__closure__) # a = 15, b = 20

About LAMBDA_CAR and LAMBDA_CDR, they return the first and the
second element of the pair, respectively.

Mental exercise: try to understand why LAMBDA_CAR and LAMBDA_CDR work!

Lists

If you paid enough attention, you noted that car, cdr and cons are the
same names that we used to define the functions that operate over lists. And
yes, they are the same! This happens because the way lists are implemented in
Church encoding.

Church lists just are pairs where:

• the first element is the first element of the list
• the second element is a list with the rest of the elements

That is a recursive definition where the base of the recursion (an empty
list) can be implemented by many ways. Here we are using to represent an empty
list the boolean LAMBDA_FALSE:

LAMBDA_EMPTY = LAMBDA_FALSE

This way, a list with the values [1, 2, 3] can be declared this way:

LAMBDA_CONS(1)(LAMBDA_CONS(2)(LAMBDA_CONS(3)(LAMBDA_FALSE)))

In practice, they are recursive pairs:

(1, (2, (3, LAMBDA_EMPTY)))

So many parentheses! But note that, at this point, LAMBDA_CAR, LAMBDA_CDR
and LAMBDA_CONS, when applied to lists have the same behaviour than car,
cdr and cons that we defined to operate over Python lists:

• LAMBDA_CAR returns the first element of the first pair, this is, the first
  element of the list (1)
• LAMBDA_CDR returns the first element of the second pair, this is, the
  rest of the list ((2, (3, LAMBDA_EMPTY)))
• LAMBDA_CONS adds another pair, appending another element

As the definition of those lists is recursive, the iteration over them will also
be done in a recursive way. The function that we’ll use to know whether the
recursion has reached the end is this:

LAMBDA_ISEMPTY = lambda l: l(lambda h: lambda t: lambda d: LAMBDA_FALSE)(LAMBDA_TRUE)

That is:

• if l is empty (it is equal to LAMBDA_EMPTY), then it returns the second
  argument: LAMBDA_TRUE
• if l is not empty, then l is a pair. l is called with the function (lambda h:
lambda t: lambda d: LAMBDA_FALSE) as argument. That function discards
  everything and return LAMBDA_FALSE. Try to simulate it ;-).

Conversion

Pairs can be converted from and to Python lists that have only two
elements. The pythonic way to do that would be using tuples of size 2, but, in
order to keep the code homogeneity, I’m using lists:

def l2p(l):
    return [LAMBDA_CAR(l), LAMBDA_CDR(l)]

def p2l(p):
    return LAMBDA_CONS(p[0])(p[1])

We can also convert Python lists and Church lists:

def ll2pl(l):
    if l2b(LAMBDA_ISEMPTY(l)): return []
    return [LAMBDA_CAR(l)] + ll2pl(LAMBDA_CDR(l))

def pl2ll(l):
    if len(l) == 0: return LAMBDA_EMPTY
    return LAMBDA_CONS(l[0])(pl2ll(l[1:]))

Using Church pairs in partition

As partition returns two values (a Python tuple), we can use here a Church pair:

    # before:
    return L, R

    # after:
    return LAMBDA_CONS(L)(R)

Using Church lists in partition

Let’s use Church lists in quicksort! First of all, we’re going to convert
partition to operate over Church lists. Currently, our situation is this:

def partition(A):
    p = car(A)

    L, R = [], []

    for x in cdr(A):
        if l2b(LAMBDA_LESS(x)(p)):
            L, R = cons(x, L), R
        else:
            L, R = L, cons(x, R)
    L, R = L, cons(p, R)

    return L, R

So, we need to replace car, cdr, cons and [] by their corresponding in
lambda calculus:

def partition(A):
    p = LAMBDA_CAR(A)
    L, R = LAMBDA_EMPTY, LAMBDA_EMPTY

    for x in lliterator(LAMBDA_CDR(A)):
        if l2b(LAMBDA_LESS(x)(p)):
            L, R = LAMBDA_CONS(x)(L), R
        else:
            L, R = L, LAMBDA_CONS(x)(R)
    L, R = L, LAMBDA_CONS(p)(R)

    return LAMBDA_CONS(L)(R)

Note that I created the generator lliterator to iterate over Church lists:

def lliterator(l):
    while not l2b(LAMBDA_ISEMPTY(l)):
        yield LAMBDA_CAR(l)
        l = LAMBDA_CDR(l)

Using Church lists in quicksort

Now we’re going to add Church lists to the function quicksort! We still
need to define the function concat for Church lists. We can implement it
recursively:

• If the list on the left is empty, we need to use the list on the right
• If the list on the left is not empty, it returns a new list where:
  • the first element is the first element (car) of the list on the left
  • the rest of the list is the concatenation of the rest (cdr) of the
    list on the left with the list on the right

That is (note the currying):

def LAMBDA_CONCAT(l1):
    def _LAMBDA_CONCAT(l2):
        if l2b(LAMBDA_ISEMPTY(LAMBDA_CDR(l1))):
            return LAMBDA_CONS(LAMBDA_CAR(l1))(l2)
        else:
            return LAMBDA_CONS(LAMBDA_CAR(l1))(LAMBDA_CONCAT(LAMBDA_CDR(l1))(l2))
    return _LAMBDA_CONCAT

This is a little different to the other operations that were written in a single
expression. Spoiler: we’re going to handle this further!

Once having concat defined, we can replace all the Python list operations by
Church list operations in quicksort:

def quicksort(A):
    # len(A) <= 1
    if l2b(LAMBDA_ISEMPTY(A)): return A
    if l2b(LAMBDA_ISEMPTY(LAMBDA_CDR(A))): return A

    L, R = partition(A)
    p = LAMBDA_CAR(R)

    L = quicksort(L)
    R = quicksort(LAMBDA_CDR(R))

    return LAMBDA_IF(LAMBDA_ISEMPTY(L))(LAMBDA_CONS(p)(R))(LAMBDA_CONCAT(L)(LAMBDA_CONS(p)(R)))

You can see it here.

Replacing loops by recursive functions

As in lambda calculus there aren’t any states, we can’t use loops as we do
in imperative languages, that is, repeating a code snippet and changing the
state of a variable.

And due to the lack of states, instead of changing an existing value we return a
new value, just like we did when replacing the standard behaviour of
quicksort to return a sorted list instead of sort the original list.

Even when we are write code in languages that support both the functional and
imperative paradigms, like Python, if we restrict ourselves to write a code in a
functional manner we can’t use loops.

And how can we solve the problems that would be solved using loops? There are
many solutions depending on the case, for example, we could use reduce, list
comprehensions, map, filter, recursive functions, etc. In this quicksort
we only have one loop, in partition. We’re going to replace it by a
recursive function.

Replacing for by while

Currently, the loop is this:

p = LAMBDA_CAR(A)
L, R = LAMBDA_EMPTY, LAMBDA_EMPTY

for x in lliterator(LAMBDA_CDR(A)):
    if l2b(LAMBDA_LESS(x)(p)):
        L, R = LAMBDA_CONS(x)(L), R
    else:
        L, R = L, LAMBDA_CONS(x)(R)

After removing the iterator lliterator and replacing the for by a while,
we get this:

p = LAMBDA_CAR(A)
L, R = LAMBDA_EMPTY, LAMBDA_EMPTY

S = LAMBDA_CDR(A)
while True:
    if l2b(LAMBDA_ISEMPTY(S)): break
    x = LAMBDA_CAR(S)
    if l2b(LAMBDA_LESS(x)(p)):
        L, R = LAMBDA_CONS(x)(L), R
    else:
        L, R = L, LAMBDA_CONS(x)(R)
    S = LAMBDA_CDR(S)

In other words: at first S is equal to the input list without the first
element (the pivot p). Each iteration of while removes a value from S
and stores it in x. If x < p, we append x to the beginning of L, otherwise
we append to the end of R. The stop condition is when the list S is empty.

For now on we can identify the elements that will be useful for writing this
loop as a recursive function:

• the inputs L and R that are, at first, empty Church lists;
• the input S that is, at first, equal to LAMBDA_CDR(A);
• the outputs, that are the values of L and R at the end of the loop;
• the stop condition, that are when S is empty.

Converting while to recursion

Cool, what we have so far is enough to write a recursive function (that I’m
calling here _partition), given the while loop code:

p = LAMBDA_CAR(A)
L, R = LAMBDA_EMPTY, LAMBDA_EMPTY

S = LAMBDA_CDR(A)

def _partition(S, L, R):
    if l2b(LAMBDA_ISEMPTY(S)): return L, R
    x = LAMBDA_CAR(S)
    if l2b(LAMBDA_LESS(x)(p)):
        nL, nR = LAMBDA_CONS(x)(L), R
    else:
        nL, nR = L, LAMBDA_CONS(x)(R)
    S = LAMBDA_CDR(S)
    return _partition(S, nL, nR)

nL, nR = _partition(S, L, R)

Note that _partition doesn’t change the state of the inputs L and
R. Instead of changing the original input data, it returns new data that
are stored in the variables nL and nR, that are the L and R arguments of
the next recursive call.

We can also make that function return Church pairs instead of tuples:

p = LAMBDA_CAR(A)
L, R = LAMBDA_EMPTY, LAMBDA_EMPTY

S = LAMBDA_CDR(A)

def _partition(S, L, R):
    if l2b(LAMBDA_ISEMPTY(S)): return LAMBDA_CONS(L)(R)
    x = LAMBDA_CAR(S)
    if l2b(LAMBDA_LESS(x)(p)):
        nL, nR = LAMBDA_CONS(x)(L), R
    else:
        nL, nR = L, LAMBDA_CONS(x)(R)
    S = LAMBDA_CDR(S)
    return _partition(S, L, R)

LR = _partition(S, L, R)
nL, nR = LAMBDA_CAR(LR), LAMBDA_CDR(LR)

You can see it here.

Replacing variables by lets

A let expression allows us to
define a value to a variable inside a scope so that its value will never
be changed. In Python, this concept makes little sense, but it is implemented
in many ways by different languages. I’ll show you some of them.

Starting by Kotlin, let is a method that can be called by any object so
we can assign a temporary name to it:

val x = 2.let { a -> 
   3.let { b ->
      a + b * a
   }
}

In Haskell, let is an expression where the first half is the value
attribution and the second half is the expression that we want to evaluate:

x = let a = 2
        b = 3
    in a + b * a

In Hy (Python with Lisp syntax), it is very close to
Haskell: first we attribute the values to the variables, then we declare the
expression that will use them:

(setv x
   (let [
      a 2
      b 3
      ]
      (+ a (* b a))
   )
)

(x will be 8 in the three examples above)

That construction is a very common in functional languages, as their variables
have a fixed value inside a scope. In addition, they are easy to be written
using lambda calculus. We can write the example above like that:

def _f(a, b):
   return a + b * a
x = _f(2, 3)

# or using lambda and currying:

x = (lambda a: lambda b: a + b * a)(2)(3)

Note that, like before, we are attributing a = 2 and b = 3 and then
calculating a + b * a.

Our mission in this step is to put all the variables that are not argument
or constants in lets, so they could be used in lambda calculus.

For now on, the code will be very unreadable, but let’s focus in an example of
how that substitution is made. In the function _partition that we defined
before, we’re going to replace x by a let. By now, this function looks like
this:

def _partition(S, L, R):
    if l2b(LAMBDA_ISEMPTY(S)): return LAMBDA_CONS(L)(R)
    x = LAMBDA_CAR(S)
    if l2b(LAMBDA_LESS(x)(p)):
        nL, nR = LAMBDA_CONS(x)(L), R
    else:
        nL, nR = L, LAMBDA_CONS(x)(R)
    S = LAMBDA_CDR(S)
    return _partition(S, L, R)

The if here only changes the values of L and R, we can write it as an
if-expression:

def _partition(S, L, R):
    if l2b(LAMBDA_ISEMPTY(S)): return LAMBDA_CONS(L)(R)
    x = LAMBDA_CAR(S)
    nL, nR = (LAMBDA_CONS(x)(L), R) if l2b(LAMBDA_LESS(x)(p)) else (L, LAMBDA_CONS(x)(R))

    S = LAMBDA_CDR(S)
    return _partition(S, nL, nR)

We’re only evaluating x in order to be used by that if-expression, so we can
use a let here:

• attribution: x = LAMBDA_CAR(S)
• expression: the if-expression that we just defined

To do that, let’s declare a new function called _partition2 that takes x as
its argument and call it soon after, passing as the argument x = LAMBDA_CAR(S):

def _partition(S, L, R):
    if l2b(LAMBDA_ISEMPTY(S)): return LAMBDA_CONS(L)(R)

    def _partition2(x):
        return (LAMBDA_CONS(x)(L), R) if l2b(LAMBDA_LESS(x)(p)) else (L, LAMBDA_CONS(x)(R))

    nL, nR = _partition2(LAMBDA_CAR(S))

    S = LAMBDA_CDR(S)
    return _partition(S, nL, nR)

We have a let! We can also replace the tuple by a Church pair:

def _partition(S, L, R):
    if l2b(LAMBDA_ISEMPTY(S)): return LAMBDA_CONS(L)(R)

    def _partition2(x):
        return LAMBDA_CONS(LAMBDA_CONS(x)(L))(R) if l2b(LAMBDA_LESS(x)(p)) else LAMBDA_CONS(L)(LAMBDA_CONS(x)(R))

    LR = _partition2(LAMBDA_CAR(S))
    nL, nR = LAMBDA_CAR(LR), LAMBDA_CDR(LR)

    return _partition(LAMBDA_CDR(S), nL, nR)

You can see it here.

Rewriting functions using lambda

At this point, having all the variables replaced by let, the partition and
quicksort functions don’t have variables anymore. They only have some ifs,
the return expression, and the definition of internal functions used by the
lets (and they have the same characteristics).

Take a look at this (yeah, only a look because this code is unreadable):

def quicksort(A):
    if l2b(LAMBDA_ISEMPTY(A)): return A
    if l2b(LAMBDA_ISEMPTY(LAMBDA_CDR(A))): return A

    def _quicksort(A, LR):
        return LAMBDA_IF(LAMBDA_ISEMPTY(quicksort(LAMBDA_CAR(LR))))(LAMBDA_CONS(LAMBDA_CAR(LAMBDA_CDR(LR)))(quicksort(LAMBDA_CDR(LAMBDA_CDR(LR)))))(LAMBDA_CONCAT(quicksort(LAMBDA_CAR(LR)))(LAMBDA_CONS(LAMBDA_CAR(LAMBDA_CDR(LR)))(quicksort(LAMBDA_CDR(LAMBDA_CDR(LR))))))

    return _quicksort(A, partition(A))

def partition(A):
    def _partition(S, L, R, p):
        if l2b(LAMBDA_ISEMPTY(S)): return LAMBDA_CONS(L)(R)
        def _partition2(x, L, R, p):
            if l2b(LAMBDA_LESS(x)(p)): return LAMBDA_CONS(LAMBDA_CONS(x)(L))(R)
            else: return LAMBDA_CONS(L)(LAMBDA_CONS(x)(R))

        def _partition3(S, LR, p):
            return _partition(LAMBDA_CDR(S), LAMBDA_CAR(LR), LAMBDA_CDR(LR), p)

        return _partition3(S, _partition2(LAMBDA_CAR(S), L, R, p), p)

    def _partition4(LR):
        return LAMBDA_CONS(LAMBDA_CAR(LR))(LAMBDA_CONS(LAMBDA_CAR(A))(LAMBDA_CDR(LR)))

    return _partition4(_partition(LAMBDA_CDR(A), LAMBDA_EMPTY, LAMBDA_EMPTY, LAMBDA_CAR(A)))

We can replace all the ifs by if-expressions and those if-expressions
by LAMBDA_IF that we defined using Church booleans. Besides that, the
internal functions can be defined using lambda instead of def as they
only have the return expression. Now we have this awful code:

def quicksort(A):
    _quicksort = lambda A: lambda LR: LAMBDA_CONCAT(quicksort(LAMBDA_CAR(LR)))(LAMBDA_CONS(LAMBDA_CAR(LAMBDA_CDR(LR)))(quicksort(LAMBDA_CDR(LAMBDA_CDR(LR)))))

    _quicksort2 = lambda A: LAMBDA_IF(LAMBDA_ISEMPTY(A))(lambda A: A)(lambda A: LAMBDA_IF(LAMBDA_ISEMPTY(LAMBDA_CDR(A)))(A)(_quicksort(A)(partition(A))))

    return _quicksort2(A)(A)

def partition(A):
    _partition2 = lambda x: lambda L: lambda R: lambda p: LAMBDA_IF(LAMBDA_LESS(x)(p))(LAMBDA_CONS(LAMBDA_CONS(x)(L))(R))(LAMBDA_CONS(L)(LAMBDA_CONS(x)(R)))

    _partition3 = lambda S: lambda LR: lambda p: _partition(LAMBDA_CDR(S))(LAMBDA_CAR(LR))(LAMBDA_CDR(LR))(p)

    _partition = (lambda S: LAMBDA_IF(LAMBDA_ISEMPTY(S))(lambda L: lambda R: lambda p: LAMBDA_CONS(L)(R))(lambda L: lambda R: lambda p: _partition3(S)(_partition2(LAMBDA_CAR(S))(L)(R)(p))(p)))

    _partition4 = (lambda A: lambda LR: LAMBDA_CONS(LAMBDA_CAR(LR))(LAMBDA_CONS(LAMBDA_CAR(A))(LAMBDA_CDR(LR))))(A)

    return _partition4(_partition(LAMBDA_CDR(A))(LAMBDA_EMPTY)(LAMBDA_EMPTY)(LAMBDA_CAR(A)))

In this case, the internal functions (even though they are now variables) can be
constants. This way, they don’t need to be inside quicksort and
partition that could only have the return expression. Then, they could be
written using lambda instead of def:

_quicksort = lambda A: lambda LR: LAMBDA_CONCAT(quicksort(LAMBDA_CAR(LR)))(LAMBDA_CONS(LAMBDA_CAR(LAMBDA_CDR(LR)))(quicksort(LAMBDA_CDR(LAMBDA_CDR(LR)))))
_quicksort2 = lambda A: LAMBDA_IF(LAMBDA_ISEMPTY(A))(lambda A: A)(lambda A: LAMBDA_IF(LAMBDA_ISEMPTY(LAMBDA_CDR(A)))(A)(_quicksort(A)(partition(A))))
quicksort = lambda A: _quicksort2(A)(A)
_partition2 = lambda x: lambda L: lambda R: lambda p: LAMBDA_IF(LAMBDA_LESS(x)(p))(LAMBDA_CONS(LAMBDA_CONS(x)(L))(R))(LAMBDA_CONS(L)(LAMBDA_CONS(x)(R)))
_partition3 = lambda S: lambda LR: lambda p: _partition(LAMBDA_CDR(S))(LAMBDA_CAR(LR))(LAMBDA_CDR(LR))(p)
_partition = (lambda S: LAMBDA_IF(LAMBDA_ISEMPTY(S))(lambda L: lambda R: lambda p: LAMBDA_CONS(L)(R))(lambda L: lambda R: lambda p: _partition3(S)(_partition2(LAMBDA_CAR(S))(L)(R)(p))(p)))
_partition4 = (lambda A: lambda LR: LAMBDA_CONS(LAMBDA_CAR(LR))(LAMBDA_CONS(LAMBDA_CAR(A))(LAMBDA_CDR(LR))))
partition = lambda A:_partition4(A)(_partition(LAMBDA_CDR(A))(LAMBDA_EMPTY)(LAMBDA_EMPTY)(LAMBDA_CAR(A)))

Recursion and Y combinator

Some of those lambda functions are recursive:

• quicksort calls _quicksort2 that calls quicksort
• _partition calls _partition3 that calls _partition

However, a property of lambda calculus is that a function doesn’t need to have
a name. But how can a function reference itself without knowing its name? The
answer is Y Combinator.

To illustrate Y combinator, take a look at this factorial function:

def fac(n):
   return 1 if n == 0 else n * fac(n-1)

# using lambda:
fac = lambda n: 1 if n == 0 else n * fac(n-1)

Then we can use Y combinator to replace the fac call:

fac = (lambda f: f(f))(lambda f: lambda n: 1 if n == 0 else n * f(f)(n-1))

# we even don't need to name fac. This expression calculates 5! = 120 recursively:
(lambda f: f(f))(lambda f: lambda n: 1 if n == 0 else n * f(f)(n-1))(5)

What happens inside that thing? Note that we have a function (lambda f: lambda n: 1 if
n == 0 else n * f(f)(n-1)), very similar to the original fac, except that
it takes an argument f and calls f(f) instead of fac. The idea of Y
combinator here is that f will always be the same function and that it
passes itself as an argument, recursively, in order to the allow the
recursive calls to make another recursive calls. Who will guarantee the base
of that recursion is (lambda f: f(f)), that will provide the first passing of
that function to itself.

Mental exercise: try to simulate fac(2) and see the magic happening.

Using Y combinator

Ok, now we can replace the recursive call in quicksort by a Y combinator. By
now it looks like this:

_quicksort2 = lambda A: LAMBDA_IF(LAMBDA_ISEMPTY(A))(lambda A: A)(lambda A: LAMBDA_IF(LAMBDA_ISEMPTY(LAMBDA_CDR(A)))(A)(_quicksort(A)(partition(A))))
quicksort = lambda A: _quicksort2(A)(A)

And if we replace it by Y combinator:

_quicksort2 = lambda r: lambda A: LAMBDA_IF(LAMBDA_ISEMPTY(A))(lambda A: A)(lambda A: LAMBDA_IF(LAMBDA_ISEMPTY(LAMBDA_CDR(A)))(A)(_quicksort(r)(A)(partition(A))))
quicksort = (lambda r: r(r)) lambda A: _quicksort2(r)(A)(A)

Mental exercise: the quicksort call is not in quicksort itself but in
_quicksort2 (that is called by quicksort). Can you figure out how Y
combinator is used in that situation?

You can see it here.

Expanding everything!

At this point, all the values, data structures and ifs are
functions. Also, those functions and all the others are values that can be
written in a single expression.

Our work here is, basically, replace all the constants by their values
so that quicksort can be a single expression. This can be done using the text
replacement tool of a text editor.

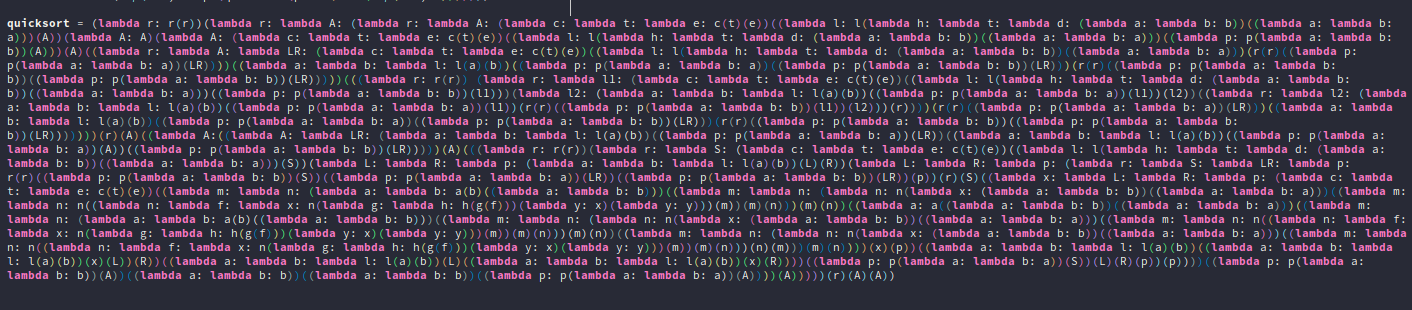
Finally we have this awful thing:

quicksort = (lambda r: r(r))(lambda r: lambda A: (lambda r: lambda A: (lambda c: lambda t: lambda e: c(t)(e))((lambda l: l(lambda h: lambda t: lambda d: (lambda a: lambda b: b))((lambda a: lambda b: a)))(A))(lambda A: A)(lambda A: (lambda c: lambda t: lambda e: c(t)(e))((lambda l: l(lambda h: lambda t: lambda d: (lambda a: lambda b: b))((lambda a: lambda b: a)))((lambda p: p(lambda a: lambda b: b))(A)))(A)((lambda r: lambda A: lambda LR: (lambda c: lambda t: lambda e: c(t)(e))((lambda l: l(lambda h: lambda t: lambda d: (lambda a: lambda b: b))((lambda a: lambda b: a)))(r(r)((lambda p: p(lambda a: lambda b: a))(LR))))((lambda a: lambda b: lambda l: l(a)(b))((lambda p: p(lambda a: lambda b: a))((lambda p: p(lambda a: lambda b: b))(LR)))(r(r)((lambda p: p(lambda a: lambda b: b))((lambda p: p(lambda a: lambda b: b))(LR)))))(((lambda r: r(r)) (lambda r: lambda l1: (lambda c: lambda t: lambda e: c(t)(e))((lambda l: l(lambda h: lambda t: lambda d: (lambda a: lambda b: b))((lambda a: lambda b: a)))((lambda p: p(lambda a: lambda b: b))(l1)))(lambda l2: (lambda a: lambda b: lambda l: l(a)(b))((lambda p: p(lambda a: lambda b: a))(l1))(l2))((lambda r: lambda l2: (lambda a: lambda b: lambda l: l(a)(b))((lambda p: p(lambda a: lambda b: a))(l1))(r(r)((lambda p: p(lambda a: lambda b: b))(l1))(l2)))(r))))(r(r)((lambda p: p(lambda a: lambda b: a))(LR)))((lambda a: lambda b: lambda l: l(a)(b))((lambda p: p(lambda a: lambda b: a))((lambda p: p(lambda a: lambda b: b))(LR)))(r(r)((lambda p: p(lambda a: lambda b: b))((lambda p: p(lambda a: lambda b: b))(LR)))))))(r)(A)((lambda A:((lambda A: lambda LR: (lambda a: lambda b: lambda l: l(a)(b))((lambda p: p(lambda a: lambda b: a))(LR))((lambda a: lambda b: lambda l: l(a)(b))((lambda p: p(lambda a: lambda b: a))(A))((lambda p: p(lambda a: lambda b: b))(LR)))))(A)(((lambda r: r(r))(lambda r: lambda S: (lambda c: lambda t: lambda e: c(t)(e))((lambda l: l(lambda h: lambda t: lambda d: (lambda a: lambda b: b))((lambda a: lambda b: a)))(S))(lambda L: lambda R: lambda p: (lambda a: lambda b: lambda l: l(a)(b))(L)(R))(lambda L: lambda R: lambda p: (lambda r: lambda S: lambda LR: lambda p: r(r)((lambda p: p(lambda a: lambda b: b))(S))((lambda p: p(lambda a: lambda b: a))(LR))((lambda p: p(lambda a: lambda b: b))(LR))(p))(r)(S)((lambda x: lambda L: lambda R: lambda p: (lambda c: lambda t: lambda e: c(t)(e))((lambda m: lambda n: (lambda a: lambda b: a(b)((lambda a: lambda b: b)))((lambda m: lambda n: (lambda n: n(lambda x: (lambda a: lambda b: b))((lambda a: lambda b: a)))((lambda m: lambda n: n((lambda n: lambda f: lambda x: n(lambda g: lambda h: h(g(f)))(lambda y: x)(lambda y: y)))(m))(m)(n)))(m)(n))((lambda a: a((lambda a: lambda b: b))((lambda a: lambda b: a)))((lambda m: lambda n: (lambda a: lambda b: a(b)((lambda a: lambda b: b)))((lambda m: lambda n: (lambda n: n(lambda x: (lambda a: lambda b: b))((lambda a: lambda b: a)))((lambda m: lambda n: n((lambda n: lambda f: lambda x: n(lambda g: lambda h: h(g(f)))(lambda y: x)(lambda y: y)))(m))(m)(n)))(m)(n))((lambda m: lambda n: (lambda n: n(lambda x: (lambda a: lambda b: b))((lambda a: lambda b: a)))((lambda m: lambda n: n((lambda n: lambda f: lambda x: n(lambda g: lambda h: h(g(f)))(lambda y: x)(lambda y: y)))(m))(m)(n)))(n)(m)))(m)(n))))(x)(p))((lambda a: lambda b: lambda l: l(a)(b))((lambda a: lambda b: lambda l: l(a)(b))(x)(L))(R))((lambda a: lambda b: lambda l: l(a)(b))(L)((lambda a: lambda b: lambda l: l(a)(b))(x)(R))))((lambda p: p(lambda a: lambda b: a))(S))(L)(R)(p))(p))))((lambda p: p(lambda a: lambda b: b))(A))((lambda a: lambda b: b))((lambda a: lambda b: b))((lambda p: p(lambda a: lambda b: a))(A))))(A)))))(r)(A)(A))

Using lambdasort

Of course we can’t use this quicksort by itself in a list as it operates in
Church encoding. We’ll need a wrapper to translate the Python types to Church
encoding, sort the Church list using quicksort and then translate it back to a
Python list. We’re going to use the previous functions.

def quicksort_wrapper(A):
    church = pl2ll([i2l(x) for x in A])
    sorted_church = quicksort(church)
    return [l2i(x) for x in ll2pl(sorted_church)]

Now you can use quicksort_wrapper to sort your list and it will use our
lambdasort as backend:

>>> from lambdasort import quicksort_wrapper
>>> x = [22, 33, 11, 55, 99, 11, 33, 77, 44]
>>> quicksort_wrapper(x)
[11, 11, 22, 33, 33, 44, 55, 77, 99]

Final thoughts

I wrote lambdasort in 2017 (my third year of university) in just two intense
days, after a class by Professor Gubi
about lambda calculus and Y
combinator. He told us about Programming with Nothing, mentioned earlier. I
found it so impressive that I wanted to do something similar, and challenged
myself to write something harder then a fizzbuzz, so here we are!

Write it was really fun, and I didn’t notice at first how much I learned in only
two days, and it took me years to finally write this text explaining what I
did. So, thank you for reading it!

Last but not least, English is not my first language and I’m trying to make my
best efforts to keep my personal page in both Portuguese and English. So, if you
find something wrong about it or about anything here feel free to
open a issue.