Hanxun Jin (a,b), Horacio D. Espinosa (b)

a Division of Engineering and Applied Science, California Institute of Technology

b Department of Mechanical Engineering, Northwestern University

Modified from the following publication:

Hanxun Jin, Enrui Zhang, and Horacio D. Espinosa, Recent Advances and Applications of Machine Learning in Experimental Solid Mechanics: A Review, Applied Mechanics Reviews, 2023, 75(6), 061001.(https://doi.org/10.1115/1.4062966)

In recent years, Machine Learning (ML) has become increasingly prominent in Solid Mechanics. Its diverse applications include extracting unknown material parameters, developing surrogate models for constitutive modeling, advancing multiscale modeling, and designing architected materials. The iMechanica Journal Club has featured several posts on these applications, beginning with Prof. Miguel Bessa’s insightful introduction in February 2020 (https://imechanica.org/node/23957), followed by Prof. Wei Gao’s comprehensive discussion of ML in atomistic materials modeling in November 2021 (https://imechanica.org/node/25544), Prof. Emma Lejeune’s May 2022 discussion on the curating mechanical datasets (https://imechanica.org/node/25935), and Prof. Nikolas Bouklas’s June 2023 examination of ML in constitutive modeling and computational mechanics (https://imechanica.org/node/25544). In this Journal Club, we will focus our discussion on the recent advances and challenges of ML when experimental data is involved. With broad community interest, as reflected by the increasing number of publications in this field, we have recently published a review article in Applied Mechanics Reviews titled “Recent Advances and Applications of Machine Learning in Experimental Solid Mechanics: A Review” [1]. Moreover, a recent insightful paper from Prof. Sam Daly’s group also discussed some perspectives in this field [2]. In this Journal Club, we would like to introduce and share insights into this exciting field. For more detailed discussions, please refer to these publications [1-2].

1.    Motivation: What ML can help for experimental solid mechanics?

The field of experimental solid mechanics has continuously evolved over the years, driven by the need to characterize and understand the mechanical properties of both natural and artificial materials and structures [3, 4]. This evolution has led to the development of various experimental apparatuses and measurement techniques applicable across multiple length and time scales. Such technological advancements have resulted in the generation of an extensive and ever-increasing amount of experimental data. Therefore, employing fast and robust ML algorithms in experimental mechanics is becoming increasingly crucial. The application of ML in experimental mechanics does more than just identify deformation fields and material properties; it also facilitates the development of new experimental techniques, which are designed for big data generation, providing high informational content and opening new avenues in the field of solid mechanics. 

Moreover, the recent progress in the materials by design concept has led to the creation of multifunctional architected materials and high-performance 2D/3D materials/devices, supported by the rapid development of fabrication techniques like Additive Manufacturing and high throughput testing methodologies. In this context, experimental solid mechanics plays a crucial role by providing essential experimental data for training, validation, and understanding the connection between fabrication processes and mechanical properties. The integration of innovative ML algorithms with advancements in fabrication and experimental methods holds the promise of a paradigm shift in the discovery and development of novel multifunctional materials and devices. 

2.   ML framework for experimental solid mechanics

ML methods are typically data-driven, relying on extensive datasets that may include images, texts, and audio [5]. A notable example is ChatGPT [6], which utilizes a transformer language model [7] based on self-attention mechanisms to effectively process language. In engineering and physics disciplines, however, many problems are often governed by underlying physical laws such as partial differential equations (PDEs). In solid mechanics, the equilibrium, compatibility, and constitutive equations define the kinematics of continuum bodies. These physical laws can provide valuable a priori temporal or spatial information, which can be integrated into the ML training. To this end, physics-informed neural networks (PINNs) [8] have been developed by the Karniadakis group at Brown University, offering a novel approach for solving problems guided by physical laws and reducing the reliance on extensive datasets.

In the context of experimental solid mechanics, we can envision a spectrum of scientific ML methods that blend data-driven and physics-informed approaches. This spectrum can be categorized into three scenarios, as illustrated in Fig. 1: (I) physics-informed learning method [8, 9], (II) physics-based data-driven method, and (III) purely data-driven method. The physics-based data-driven approach, used when problems are too complex to be fully described by PDEs, often leverages large-scale computer simulations that incorporate physics, such as finite element analysis (FEA) or molecular dynamics (MD), to create training datasets. This approach is particularly effective for complex phenomena like cohesive fracture in solids. 

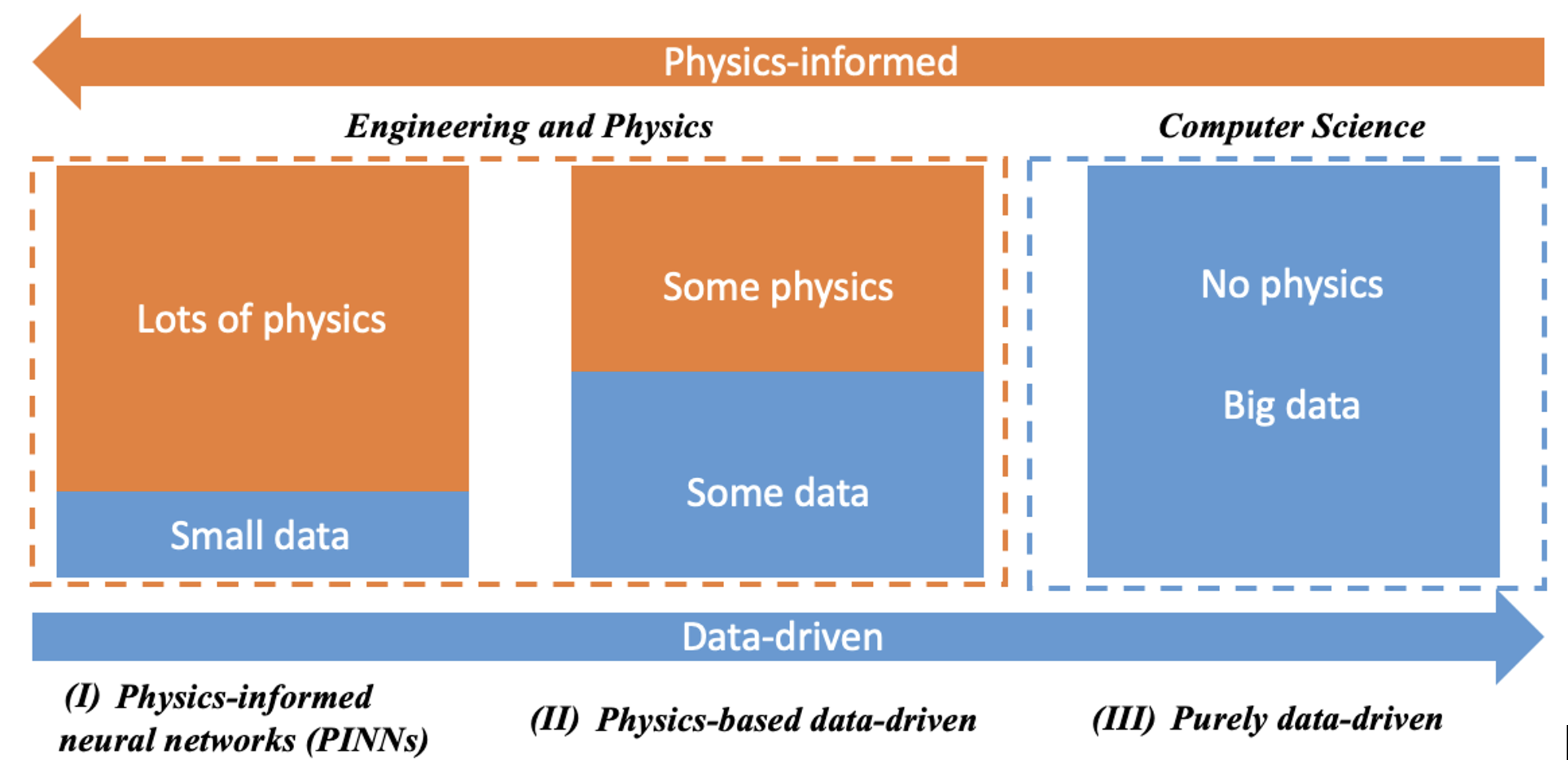
Figure 1 Schematics of three ML approaches based on available physics and data: (I) Physics-informed neural networks (PINNs); (II) Physics-based data-driven; and (III) Purely data-driven [10]. Figure idea from Karniadakis et al. [9].

 

3. Applications of ML in experimental solid mechanics

In this section, we will briefly review recent advancements of ML in experimental solid mechanics, covering a wide range of fields such as fracture mechanics, biomechanics, and architected materials. For other fields like nanomechanics and low-dimensional material characterization, the readers are referred to the review [1].

3.1 ML for fracture mechanics 

One of the ML applications in fracture mechanics is to identify fracture properties like fracture toughness or cohesive parameters from experimental data. For example, Liu et al. [11] proposed an ML approach to obtain the fracture toughness for micro-fabricated ceramic cantilevers. As shown in Fig. 2(a), when the analytical solution is not accessible due to geometry and material complexity, an ML solution trained from representative and sufficient FEM datasets can provide accurate fracture toughness. When predicting dynamic fracture toughness under ultra-high loading rates, the conventional experimental measurement of load-displacement is not accessible. To this end, Jin et al. [12] proposed an ML-assisted big-data-generating experimental framework that can accurately measure the dynamic fracture toughness and cohesive parameters of samples from plate impact experiments (Fig. 2(b)). This big-data-generating experimental framework can be easily extended to other mechanics problems, under extreme conditions, such as stress wave induced phase transformations, shear localization, and others where conventional measurement methods are not applicable. Beyond the fracture properties identification, ML is also effective in predicting internal crack/flaw geometry and locations from the experimental measurement. For example, Zhang et al. [13] applied PINNs to identify internal cracks in linear and nonlinear solids. As shown in Fig. 2(c), the framework uses the external boundary conditions as “sensors” to inversely identify the internal crack information under deformation. ML can also be used with non-destructive measurement methods to characterize internal cracks without deforming the material. For example, Niu et al. [14, 15] used FEM-trained CNN to accurately identify the internal crack information from ultrasound measurement (Fig. 2(d)). Impressively, the simulation-trained CNN can make predictions of crack shapes and locations on experimental data with an error of around 5%. 

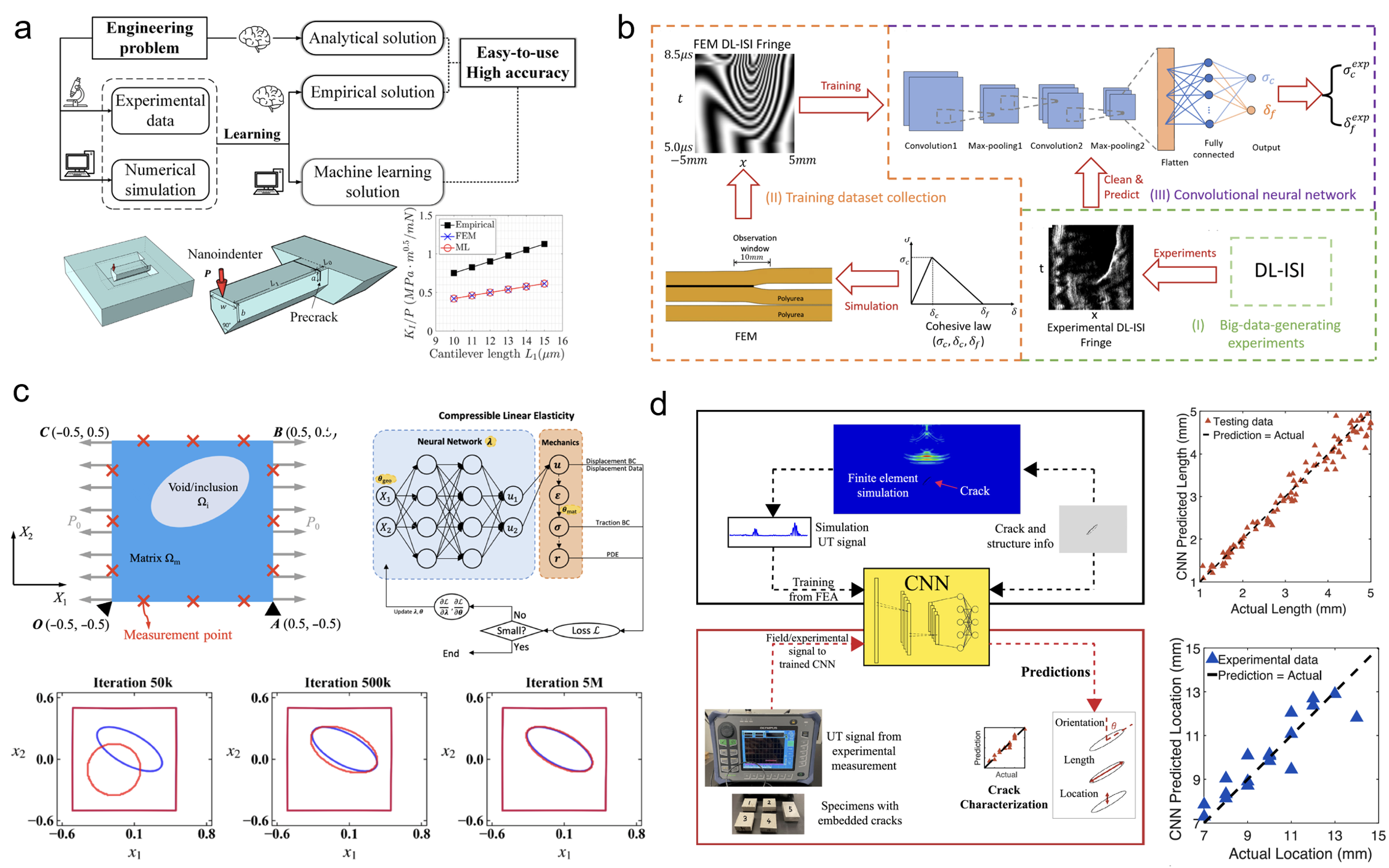
Figure 2 Applications of ML in fracture mechanics. (a) ML solutions can predict accurate fracture toughness comparable to simulations when an analytical solution is not accessible due to sample complexity [11]. (b) The CNN-based deep learning algorithm can accurately determine dynamic fracture toughness and cohesive parameters under an extremely high strain rate loading [12]. (c) PINN can identify internal voids/inclusions for linear and nonlinear solids [13]. (d) FEM simulation-trained CNN can determine crack locations and geometry in experiments [14]. 

Another recent application is to quantify the fracture toughness of low-dimensional materials through integrated in-situ electron microscopy experiments, ML, and MD simulations framework (Fig. 3(a)). Such ML and atomistic experimentation frameworks are essential in advancing the predictive power of atomistic models employed in the exploration of families of 2D materials in the spirit of the materials genome initiative. In the Espinosa group, Zhang et al. [16] performed in situ high-resolution transmission electron microscopy (HRTEM) fracture experiments to investigate the fracture toughness of two TMDs: MoS2 and MoSe2. The J-integral was computed from experimental stress-strain fields obtained from an affine transformation using HRTEM images of atomic structures surrounding the crack tip (Fig. 3(b)). To verify the experimental observations, Zhang et al. also performed MD simulations with a newly developed ML-based parametrization framework [17]. The framework proposed a parametrization framework trained from DFT datasets and an evolutionary multi-objective optimization algorithm (Fig. 3(c)). MD simulations with this potential gave similar fracture toughness as those obtained from experimental measurements. We anticipate that by integrating in-situ experiments with atomistic resolution and MD simulations with force-field parametrized based on physical ML training, the fracture behaviors of other 2D materials beyond the TMDs family, as well as other metamaterials and functional crystals, can be identified. 

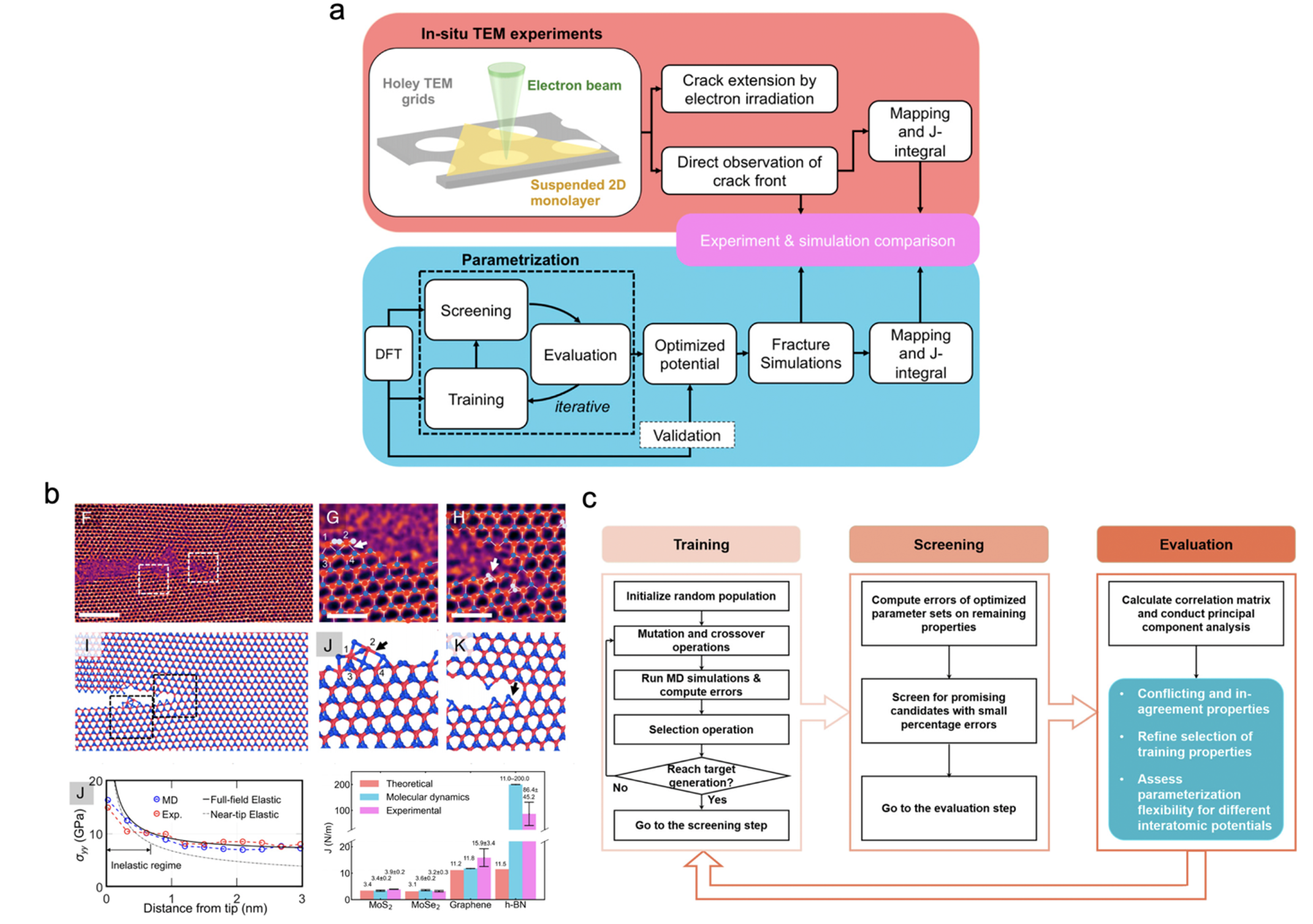
Figure 3 Applications of ML in fracture toughness characterization of 2D materials. (a) An integrated experiment-simulation framework to quantitively measure intrinsic fracture toughness of 2D materials. (b) In-situ HRTEM experiments of MoSe2 compared with MD simulations (Reproduced with permission from Ref. [16]. Copyright 2022 by National Academy of Sciences). (c) Schematic of ML-based interatomic potential parametrization approach consisting of three steps: training, screening, and evaluation (Reproduced with permission from Ref. [17] . Copyright 2021, The authors, published by Springer Nature). 

3.2  ML for biomechanics 

ML has been recently employed in biomechanics, i.e., characterizing and modeling biological materials such as tissues, blood vessels, and brain matter. Characterization of these materials from experiments and identifying constitutive models are needed to understand and predict their mechanical behaviors. Identifying these constitutive parameters for complex models from experimental data typically requires extensive nonlinear FEM and sophisticated optimization algorithms [18-20]. ML can help infer material parameters from limited experimental data with multi-modality, such as mechanical testing and microstructure data obtained from images. Recently, Holzapfel et al. [21] developed a hybrid ML model based on a residual network (ResNet) and CNN to infer three unknown material parameters for a modified HGO model [22] (Fig. 4(a)). This ML model maps second-harmonic generation (SHG) microstructure images, representing the orientation and dispersion of collagen fibers, to their mechanical stress-strain data for a total of 27 artery samples. By employing this hybrid ML model, the coefficient of determination, R2, was 0.97, while conventional least square fitting gave R2=0.676 with a much larger standard deviation. Recent advances in PINNs provide a promising alternative in constitutive parameter identification for biomaterials by encoding the underlying physics [23]. As shown in Fig. 4(b), Yin et al. [24] employed PINNs to infer the permeability and viscoelastic modulus of the thrombus. The parameters can be accurately identified by encoding these governing physics during the PINNs training. 

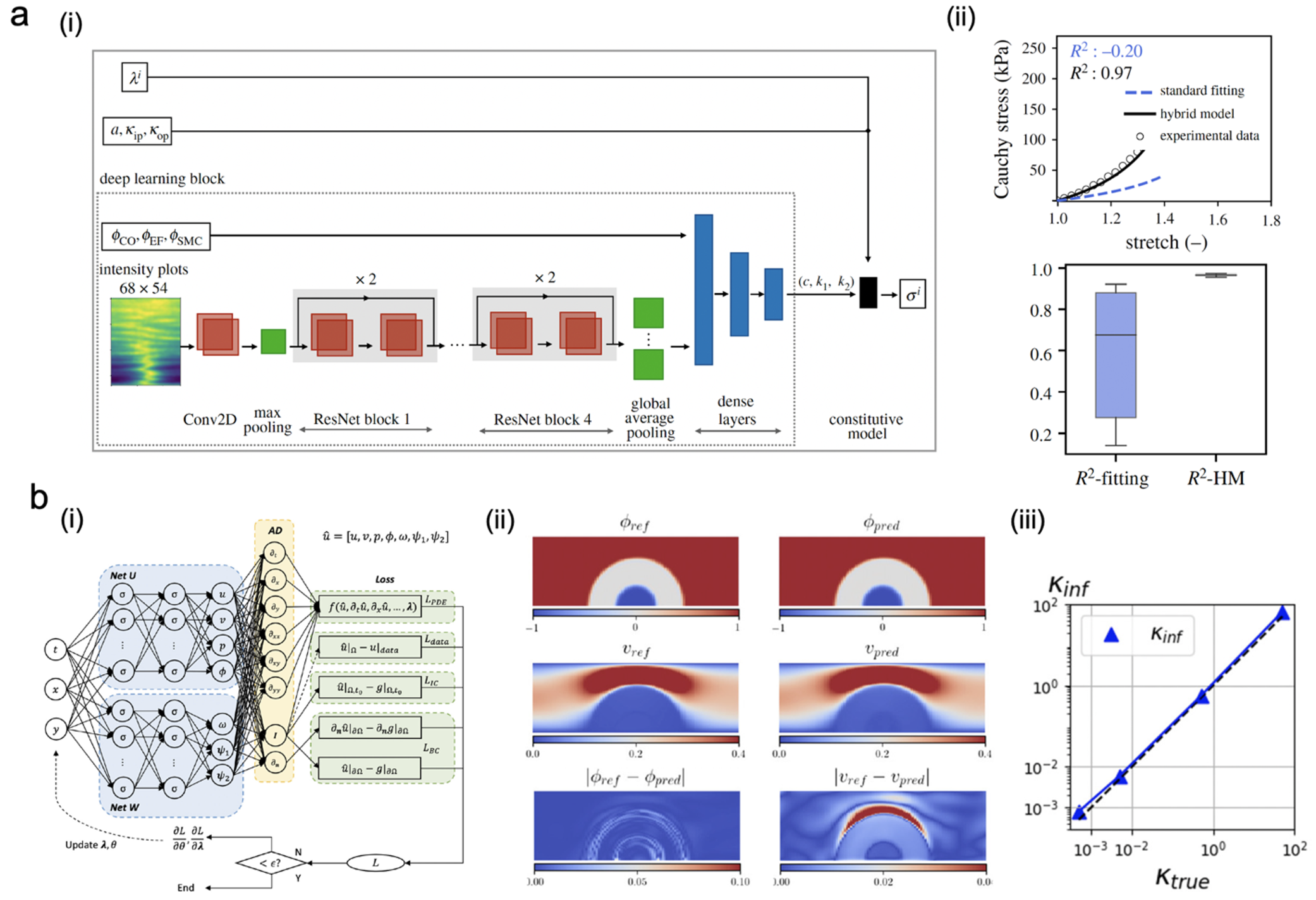
Figure 4 Applications of ML in constitutive parameter inversion for biomaterials. (a) A hybrid DL framework to identify unknown material parameters of arteries with high coefficient of determination: (i) Hybrid model architecture; (ii) Predicted stress-stretch curves from standard fitting method compared to the proposed hybrid model. (Reproduced with permission from Ref. [21]. Copyright 2021, The authors, published by the Royal Society). (b) Non-invasive inference of thrombus material parameters using PINNs: (i) Schematic of PINNs for solving inverse problem; (ii) Prediction and ground-truth of 2D flow around a thrombus; (iii) Comparison of the inferred permeability of 2D flow with the ground-truth. (Reproduced with permission from Ref. [24].  Copyright 2021 by Elsevier). 

Recently, a data-driven computation framework for constitutive modeling was proposed by Ortiz and coworkers [25-28]. In this framework, a data-driven solver directly learns the mechanical responses of materials from experimental data, which eliminates the need for complex empirical constitutive modeling. In this approach, NNs can be employed to build surrogate models of biomaterials for constitutive modeling [29-34]. Neural operators can also be employed to build data-driven surrogate models for constitutive modeling of biomaterials due to their advantage of generalizability and prediction efficiency to different inputs. For example, as shown in Fig. 5(a), Zhang et al. [35] developed a DeepONet-based model to characterize the mechanical properties of soft tissues and classify their associated genotypes from sparse and noisy experimental data. The framework could effectively learn the constitutive models from biaxial testing data for 28 mice with 4 different genotypes with an L2 error of less than 5%. More recently, You et al. [36]  employed a Fourier neural operator (FNO) based method to model soft tissues directly from experimental data (Fig. 5(b)). The method learned the material deformation model from DIC measurements and could predict the displacement field under unseen loading conditions with a relatively small error.  

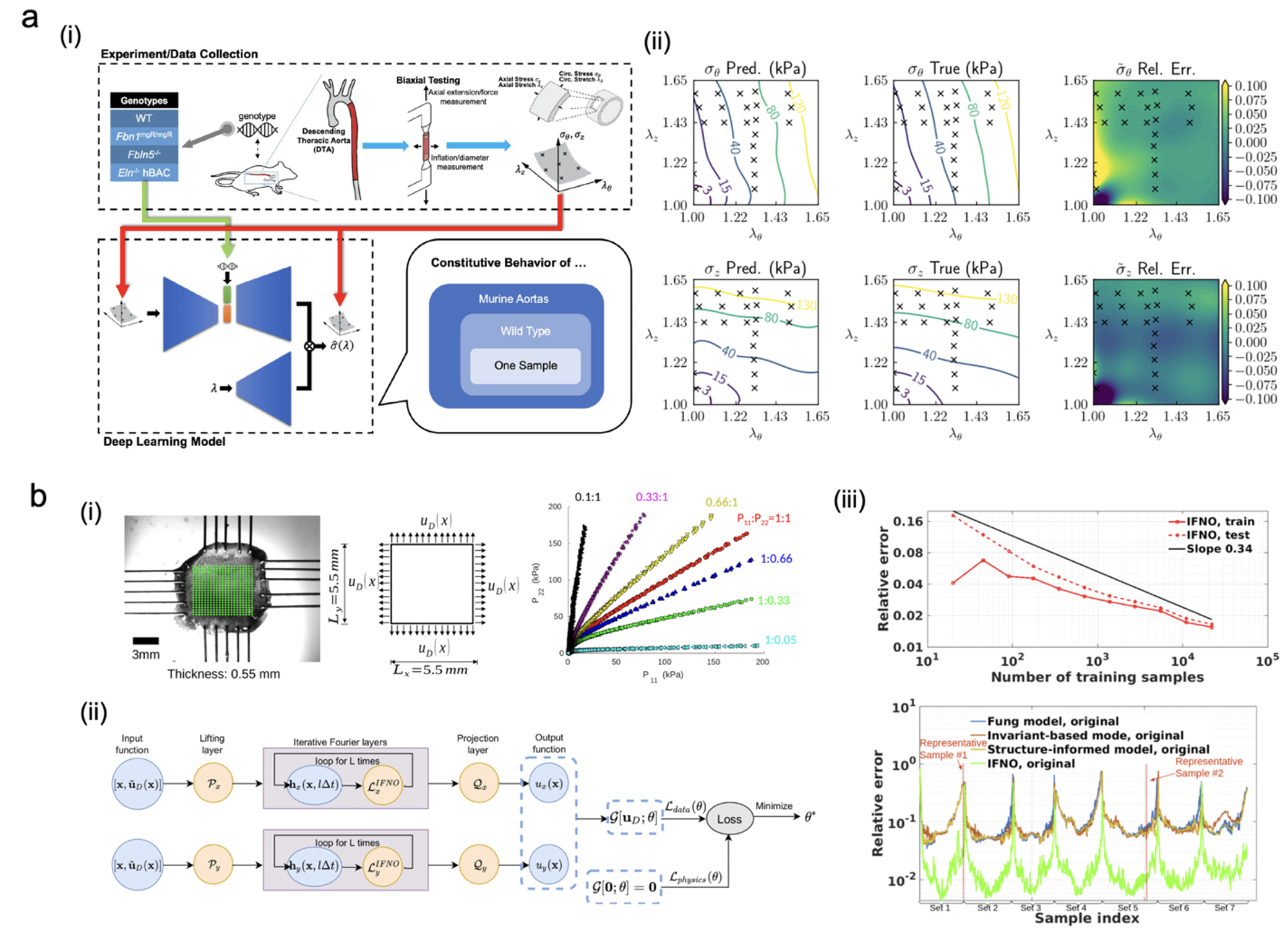
Figure 5 Applications of the neural operator in constitutive modeling of biomaterials. (a) A deepONet-based DL framework to infer biomechanical response and associated genotype of tissues: (i) the DL framework; (ii) reconstructed stress-stretch relationships compared with their true values (Reproduced with permission from Ref. [35]. Copyright 2022, The authors, published by PLOS). (b) A neural operator model to construct the mechanical response of biological tissues from displacement data measured from DIC: (i) The biaxial experimental setup; (ii) The architecture of the physics-guided Fourier neural operator; (iii) Error comparisons of proposed Fourier neural operator method and other mechanics models (Reproduced with permission from Ref. [36]. Copyright 2022 by ASME).

Another promising data-driven approach for learning constitutive laws, Efficient Unsupervised Constitutive Law Identification & Discovery (EUCLID) [37-40], was developed by the De Lorenzis group at ETH. In this framework, EUCLID leverages displacement and reaction force data rather than relying on the stress dataset. Displacement and reaction force data are readily available in experiments from digital image correlation and mechanical testing. EUCLID seeks to discover material constitutive laws as interpretable mathematical formulas. A large catalog of candidate material models is first constructed, from which dominant candidates are selected through sparse regression. The absence of stress data is compensated by using physics knowledge, specifically by minimizing the sum of squared residuals of the weak linear momentum balance. This approach allows for the discovery of unsupervised constitutive models that are physically admissible and can generalize well beyond the strain states observed in the full-field displacement data.

3.2  ML for mechanical metamaterials

ML is also becoming an important tool to systematically design novel mechanical metamaterials with desired properties and functionality [41-47]. Comprehensive review papers have been published in recent years in this field [48-51]. Here, we will focus on reviewing recent advances in experimental efforts in ML-enabled design of architected materials. One significant aspect of experimental mechanics in architected materials is to verify the predicted results of computational methods used in inverse design. For example, as shown in Fig. 6(a), Alderete and Pathak et al. [52] have proposed an ML framework that combines the K-mean clustering methods for design space reduction and a tandem NN architecture to inversely design shape-programmable 3D Kirigami metamaterials. The framework was validated by full-field experimental measurements using the shadow Moiré method [53]. A very good agreement between ML-predicted out-of-plane deformation and experiments was found under mechanical actuation. Likewise, ML can also assist in the inverse design of complex soft materials. For example, as shown in Fig. 6(b), Ma et al. [54] developed a deep residual network trained with FEM to inversely design tunable magneto-mechanical metamaterials. The predicted structures were printed and tested in good agreement with ML predictions. Moreover, GANs could also be employed to design architected structures without prior experience. For example, Mao et al. [55] used GANs to systematically design complex architected materials and found that some structures can reach Hashin-Shtrikman (HS) upper bounds. Furthermore, due to the stochastic deformation modes of metamaterials like buckling under compression, uncertainty quantification is necessary to design reliable structures. Bessa et al. [56] demonstrated that a data-driven Bayesian ML framework could enable the design of super compressible metamaterials. Experiments on multiscale 3D printed structures have also demonstrated the super compressibility predicted by simulations. 

Another important feature in this field is the ability to conduct high throughput experiments to generate high-fidelity data needed for ML training. Until now, most of the ML applications of the inverse design of architected metamaterials were based on training from simulations. However, such a simulation data-driven approach may not be reliable in complex cases. As such, there is a need to develop new ML frameworks to inverse design new metamaterials directly from limited but high-quality experimental data. Recently, Jin and Zhang et al. [57] proposed a DeepONet-based ML framework that can inversely design stochastic mechanical metamaterials directly from sparse but high-quality in-situ micro-mechanical experimental data. Then, an ML framework was employed to effectively learn a functional mapping between high-fidelity experimental stress-strain curves and microstructures. The work marks a significant advancement in the field of materials-by-design, potentially heralding a new era in the discovery and development of next-generation metamaterials with unparalleled mechanical characteristics derived directly from experimental insights. 

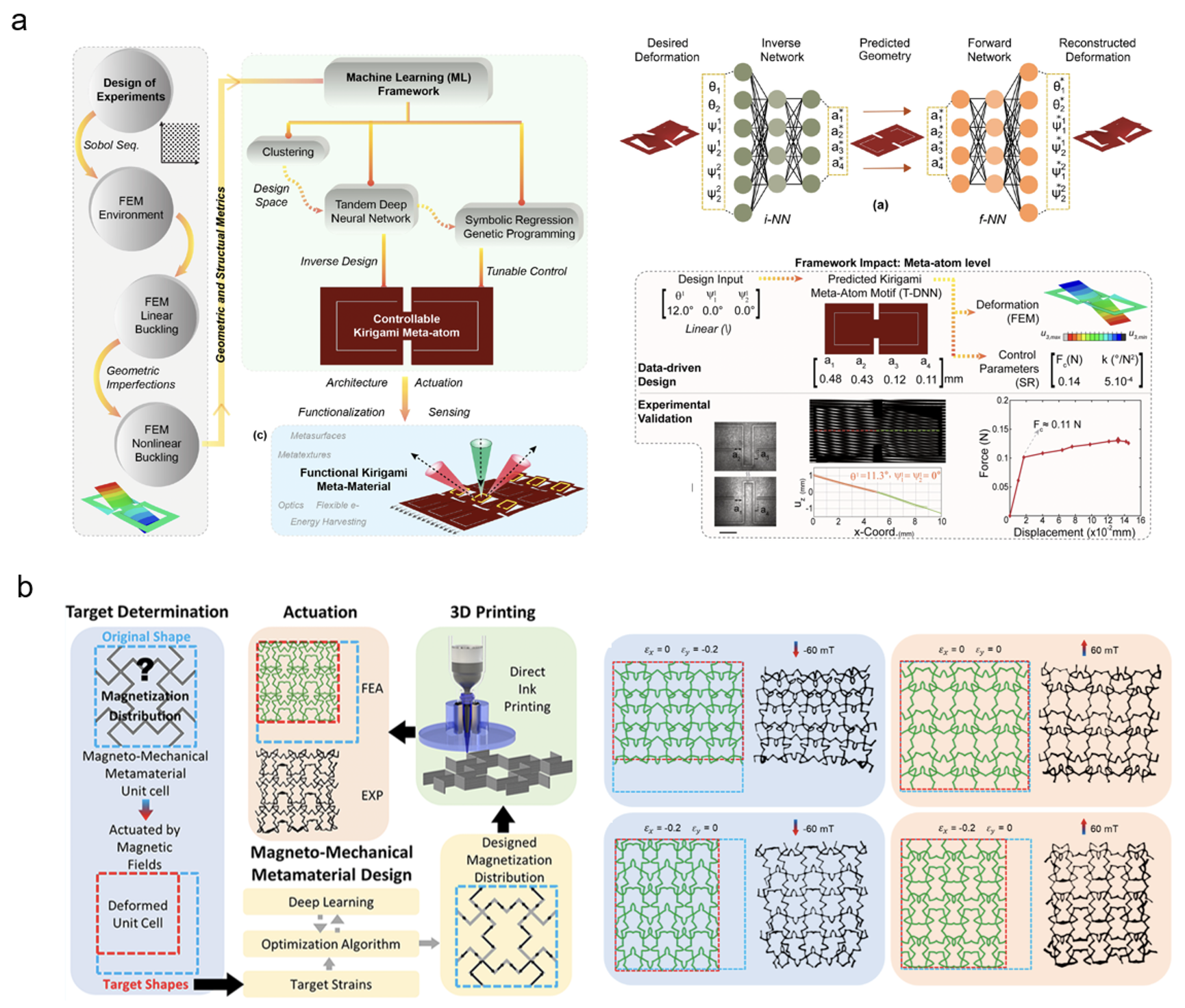
Figure 6 Applications of ML in designing architected materials. (a) An ML framework verified with experiments to inversely design shape-programmable 3D Kirigami metamaterials [52]; (b) a deep residual network (ResNet) based inverse design of tunable magneto-mechanical metamaterials [54].

4 Current challenges in applying ML for experimental solid mechanics

4.1 Integrating multi-modality and multi-fidelity experimental/computational data into ML methods

Conducting mechanical experiments, particularly those utilizing cutting-edge facilities and techniques for extremely large/small time and length scales, can be both costly and time-consuming. In many cases, researchers need to combine different experimental methods, to gain an understanding of the mechanics problem. Furthermore, computer simulations may be employed to obtain additional insights from virtual experiments. As a result, one may obtain experimental data with multi-modality and/or multi-fidelity. Multi-modal data refers to the data on an object comprising different forms and patterns, hence providing information from different channels (e.g., language data in the forms of text and speech, data on the mechanical test sample in the forms of images, and stress-strain curves). Multi-fidelity data refers to the measurement data with different levels of accuracy (e.g., high/low-resolution images of a test sample; stress-strain curves measured with load cells of different accuracies; data from real experiments and from computer simulations). Typically, high-fidelity data are expensive and hence limited, while low-fidelity data are cheap and plentiful.

To maximize the available information injected into learning algorithms, it is important to propose ML models that are capable of handling data with multi-modality [58] and multi-fidelity [59]. There have been some studies in applying such ML models to mechanics problems. For example,  Holzapfel et al. [21] seek to develop an ML method that combines microstructural information and biomechanical tests. Trask et al. [60] propose a framework that is capable of conducting multimodal inference for lattice metamaterials, relating their lattice design, stress-strain curves, and microstructural images. Lu et al. [61] designed a multi-fidelity neural network for characterizing the mechanical properties of materials in instrumented indentation. While these studies, among others, have explored multi-modality and multi-fidelity ML methods for solid mechanics problems, further investigation is still needed to better integrate data with multi-modality and multi-fidelity from experiments and/or simulations to provide deeper insights for understanding the mechanics of materials and structures. 

4.2 Quantifying and reducing the uncertainty of ML predictions

Most ML applications in experimental solid mechanics provide a point estimation – that is, a single value as the best estimate. To further acquire information regarding the reliability and confidence of such an estimation, one sometimes needs to quantify and/or reduce the uncertainty of the ML predictions. In the context of experimental solid mechanics, there are diverse sources of uncertainties coming from data and models related to almost every component in the research workflow, including: (1) experimental implementation, such as the uncertainty of material properties caused by the manufacturing of specimens, inaccurate enforcement of the experimental setup, representativeness and noisiness of data; (2) theoretical modeling, such as the misspecification/oversimplification of constitutive models, ignoring dynamic effects, ignoring length scale effects, typical in micro- and nano-mechanics, as well as continuum assumptions, neglecting material and/or geometric nonlinearity, and stochasticity; (3) numerical modeling, such as finite element discretization, inaccurate force fields in molecular dynamics simulation. On top of these three aspects of uncertainty, ML methods (especially NN-based methods) introduce a few additional sources of uncertainty, including the choices of model architecture and hyperparameters, stochasticity in the training process, and transferability of the trained model, making the accurate quantification of total uncertainty a complex and time-consuming endeavor.

Uncertainty quantification (UQ) is a discipline of science focusing on identifying, quantifying, and reducing uncertainties associated with models, numerical algorithms, experiments, and predicted outcomes or quantities of interest [62]. It is a broad area that has been studied extensively and is not exclusively applicable to machine learning methods. For detailed UQ methods and their applications in ML, readers are referred to related textbooks and review papers [63-65]. Here, we briefly review a few UQ methods that are extensively applied to estimating and reducing uncertainty in the context of ML applications in experimental solid mechanics. To quantify the uncertainty of mechanics systems, one of the most widely adopted classes of methods is the Bayesian procedure. Built upon the well-established, century-old Bayes’ theorem [66], the Bayesian procedure seeks to infer the posterior distribution of variables based on prior knowledge and measured data. Specific examples of methods involving the Bayesian approach include the use of Gaussian process regression for modeling the nonlinear behavior of solids [67], the creep behavior of concrete [68], parameter inversion from nanoindentation [69], metamaterial design [56], as well as NNs for crystal plasticity [70] and multiscale modeling of nanocomposite [71]. These studies, by employing the Bayesian procedure, provide a distribution of the quantities of interest rather than a single output. Another prevalent technique is the ensemble method, which combines a group of base models, which differ by the algorithm, hyperparameter, training data, and/or random seeds, to provide more accurate, more robust predictions. They may be applied to machine learning models such as decision trees, support vector machines, and neural networks. Through this method, one may estimate the uncertainty of the prediction according to the spread among base models as well as reduce the uncertainty by combining these models into an ensemble for enhanced predictive capability. Finally, we comment that there are still a lot of problems related to the quantification of uncertainty associated with ML applications in mechanics. It is a challenging yet worthwhile task to quantify the total uncertainty of the experimental mechanics workflow, addressing all relevant sources of uncertainty.

5 Future opportunities of ML in experimental solid mechanics 

5.1 ML for experimental mechanics under extreme conditions

In recent years, there has been an emerging interest in characterizing material properties under extreme conditions like high strain rate, high pressure, and high temperature. However, such experiments are often considered laborious and costly, requiring significant experiment preparation time. For example, in conventional plate impact experiments, which characterize dynamic properties of materials under high strain rates, the experiment preparation time (e.g., sample preparation, optical alignment, triggering circuits connection, interferometry) alone can take several days. Therefore, there is an increasing demand to design big-data-generating experiments where new high-throughput experimental techniques can be coupled with ML methods to improve the efficiency of data collection and analysis. One recent study by Jin et al. [12] demonstrated the benefits of big-data-generating experiments in the context of material dynamic fracture toughness and cohesive parameter determination. These results highlight the potential for ML to transform the field of experimental mechanics, enabling researchers to characterize material properties more efficiently and effectively under extreme conditions. Moving forward, it will be crucial to continue to develop new experimental full-field measurement techniques for experiments under extreme conditions like spatial-temporal interferometer [12] or stereo DIC [72] that can be effectively coupled with ML to generate and analyze large volumes of high-fidelity data. By leveraging ML for extreme mechanics, experimentalists will be capable of characterizing extreme material properties more efficiently and accurately, enabling new insights and applications in designing next-generation materials and technologies.

5.2 Design intelligent architected materials with in-situ decision-making capabilities

The design of materials with decision-making capability is a relatively new concept that has the potential to revolutionize material design by offering unprecedented properties. With the help of ML, architected materials can be programmed to respond to real-time stimuli based on external input. Here, we present some potential research areas in which experimental mechanics and ML can contribute to the development of these intelligent architected materials. One such area is the development of new fabrication techniques to build novel material systems with high resolution. For example, new high-throughput AM techniques, such as the hydrogel infusion AM (HIAM) method [73], can be employed to fabricate architected materials with complex geometries at a variety of scales. Furthermore, bottom-up approaches such as self-assembly can be employed to spontaneously organize nanoscale constituents into ordered structures through intermolecular forces [74, 75]. Recently, scaling-up fabrication techniques, like holographic lithography, were employed to build centimeter-size samples with nanoscale features. Another area of focus is the development of new actuation methods. Current actuation methods are mainly focused on passive actuation techniques like mechanical or electromagnetic actuation, while designing materials with active actuations that can deform on demand according to local environmental stimuli would confer intelligence to these materials. Designing materials with active actuation would involve the development of ML algorithms capable of optimizing material structures and properties based on a set of design objectives and constraints. For example, reinforcement learning algorithms could be used to train materials to learn and respond to different loading scenarios, leading to enhanced structural performance and durability. Moreover, ML algorithms could enable materials to make intelligent decisions in real-time based on environmental conditions, such as changes in temperature, humidity, or mechanical loads. This opens a wide range of potential applications for intelligent architected materials in fields such as aerospace and robotics.

6 Concluding remarks

Recent advances in ML have significantly altered the field of experimental solid mechanics, allowing for efficient and accurate experimental design, data analysis, parametric or function identification, and inverse design. There are both challenges and opportunities in this field. It is hoped that this Journal Club will provide insights and motivations for researchers in solid mechanics who are interested in employing ML to design and analyze their experiments. As the field continues to evolve, it will also be essential to build bridges to other disciplines, with the most obvious being computational mechanics, materials sciences, advanced manufacturing, and design.

References

[1] Jin, H., Zhang, E., and Espinosa, H. D., 2023, “Recent Advances and Applications of Machine Learning in Experimental Solid Mechanics: A Review,” Applied Mechanics Reviews, 75(6), p. 061001.

[2] Brodnik, N., Muir, C., Tulshibagwale, N., Rossin, J., Echlin, M., Hamel, C., Kramer, S., Pollock, T., Kiser, J., and Smith, C., 2023, “Perspective: Machine learning in experimental solid mechanics,” J Mech Phys Solids, 173, p. 105231.

[3] Sciammarella, C. A., and Sciammarella, F. M., 2012, Experimental mechanics of solids, John Wiley & Sons.

[4] Kassner, M. E., Nemat-Nasser, S., Suo, Z. G., Bao, G., Barbour, J. C., Brinson, L. C., Espinosa, H., Gao, H. J., Granick, S., Gumbsch, P., Kim, K. S., Knauss, W., Kubin, L., Langer, J., Larson, B. C., Mahadevan, L., Majumdar, A., Torquato, S., and van Swol, F., 2005, “New directions in mechanics,” Mechanics of Materials, 37(2-3), pp. 231-259.

[5] Mitchell, T. M., and Mitchell, T. M., 1997, Machine learning, McGraw-hill New York.

[6] OpenAI, 2022, “ChatGPT,” pp. https://chat.openai.com/.

[7] Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., Kaiser, Ł., and Polosukhin, I., 2017, “Attention is all you need,” Advances in neural information processing systems, 30.

[8] Raissi, M., Perdikaris, P., and Karniadakis, G. E., 2019, “Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations,” J Comput Phys, 378, pp. 686-707.

[9] Karniadakis, G. E., Kevrekidis, I. G., Lu, L., Perdikaris, P., Wang, S., and Yang, L., 2021, “Physics-informed machine learning,” Nature Reviews Physics, 3(6), pp. 422-440.

[10] Jin, H., 2021, “Big-Data-Driven Multi-Scale Experimental Study of Nanostructured Block Copolymer’s Dynamic Toughness,” Ph.D., Brown University.

[11] Liu, X., Athanasiou, C. E., Padture, N. P., Sheldon, B. W., and Gao, H. J., 2020, “A machine learning approach to fracture mechanics problems,” Acta Mater, 190, pp. 105-112.

[12] Jin, H., Jiao, T., Clifton, R. J., and Kim, K.-S., 2022, “Dynamic fracture of a bicontinuously nanostructured copolymer: A deep-learning analysis of big-data-generating experiment,” J Mech Phys Solids, 164, p. 104898.

[13] Zhang, E. R., Dao, M., Karniadakis, G. E., and Suresh, S., 2022, “Analyses of internal structures and defects in materials using physics-informed neural networks,” Sci Adv, 8(7).

[14] Niu, S. J., and Srivastava, V., 2022, “Simulation trained CNN for accurate embedded crack length, location, and orientation from ultrasound measurements,” International Journal of Solids and Structures, 242.

[15] Niu, S., and Srivastava, V., 2022, “Ultrasound classification of interacting flaws using finite element simulations and convolutional neural network,” Engineering with Computers, 38(5), pp. 4653-4662.

[16] Zhang, X., Nguyen, H., Zhang, X., Ajayan, P. M., Wen, J., and Espinosa, H. D., 2022, “Atomistic measurement and modeling of intrinsic fracture toughness of two-dimensional materials,” Proceedings of the National Academy of Sciences, 119(45), p. e2206756119.

[17] Zhang, X., Nguyen, H., Paci, J. T., Sankaranarayanan, S. K. R. S., Mendoza-Cortes, J. L., and Espinosa, H. D., 2021, “Multi-objective parametrization of interatomic potentials for large deformation pathways and fracture of two-dimensional materials,” Npj Comput Mater, 7(1).

[18] Shi, L., Yao, W., Gan, Y., Zhao, L. Y., Eugene McKee, W., Vink, J., Wapner, R. J., Hendon, C. P., and Myers, K., 2019, “Anisotropic material characterization of human cervix tissue based on indentation and inverse finite element analysis,” Journal of biomechanical engineering, 141(9).

[19] Kakaletsis, S., Meador, W. D., Mathur, M., Sugerman, G. P., Jazwiec, T., Malinowski, M., Lejeune, E., Timek, T. A., and Rausch, M. K., 2021, “Right ventricular myocardial mechanics: Multi-modal deformation, microstructure, modeling, and comparison to the left ventricle,” Acta biomaterialia, 123, pp. 154-166.

[20] Sugerman, G. P., Kakaletsis, S., Thakkar, P., Chokshi, A., Parekh, S. H., and Rausch, M. K., 2021, “A whole blood thrombus mimic: constitutive behavior under simple shear,” journal of the mechanical behavior of biomedical materials, 115, p. 104216.

[21] Holzapfel, G. A., Linka, K., Sherifova, S., and Cyron, C. J., 2021, “Predictive constitutive modelling of arteries by deep learning,” Journal of the Royal Society Interface, 18(182), p. 20210411.

[22] Holzapfel, G. A., Niestrawska, J. A., Ogden, R. W., Reinisch, A. J., and Schriefl, A. J., 2015, “Modelling non-symmetric collagen fibre dispersion in arterial walls,” Journal of the royal society interface, 12(106), p. 20150188.

[23] Song, S., and Jin, H., 2023, “Identifying Constitutive Parameters for Complex Hyperelastic Solids using Physics-Informed Neural Networks,” arXiv preprint arXiv:2308.15640.

[24] Yin, M., Zheng, X., Humphrey, J. D., and Karniadakis, G. E., 2021, “Non-invasive inference of thrombus material properties with physics-informed neural networks,” Comput Method Appl M, 375, p. 113603.

[25] Kirchdoerfer, T., and Ortiz, M., 2016, “Data-driven computational mechanics,” Comput Method Appl M, 304, pp. 81-101.

[26] Eggersmann, R., Kirchdoerfer, T., Reese, S., Stainier, L., and Ortiz, M., 2019, “Model-free data-driven inelasticity,” Comput Method Appl M, 350, pp. 81-99.

[27] Stainier, L., Leygue, A., and Ortiz, M., 2019, “Model-free data-driven methods in mechanics: material data identification and solvers,” Computational Mechanics, 64(2), pp. 381-393.

[28] Prume, E., Reese, S., and Ortiz, M., 2023, “Model-free Data-Driven inference in computational mechanics,” Comput Method Appl M, 403, p. 115704.

[29] Tac, V., Sree, V. D., Rausch, M. K., and Tepole, A. B., 2022, “Data-driven modeling of the mechanical behavior of anisotropic soft biological tissue,” Engineering with Computers, 38(5), pp. 4167-4182.

[30] He, Q., Laurence, D. W., Lee, C.-H., and Chen, J.-S., 2021, “Manifold learning based data-driven modeling for soft biological tissues,” Journal of biomechanics, 117, p. 110124.

[31] Linka, K., Hillgärtner, M., Abdolazizi, K. P., Aydin, R. C., Itskov, M., and Cyron, C. J., 2021, “Constitutive artificial neural networks: A fast and general approach to predictive data-driven constitutive modeling by deep learning,” J Comput Phys, 429, p. 110010.

[32] Masi, F., Stefanou, I., Vannucci, P., and Maffi-Berthier, V., 2021, “Thermodynamics-based Artificial Neural Networks for constitutive modeling,” J Mech Phys Solids, 147.

[33] Li, L., and Chen, C., 2022, “Equilibrium-based convolution neural networks for constitutive modeling of hyperelastic materials,” J Mech Phys Solids, 164, p. 104931.

[34] Wang, J., Li, T., Cui, F., Hui, C.-Y., Yeo, J., and Zehnder, A. T., 2021, “Metamodeling of constitutive model using Gaussian process machine learning,” J Mech Phys Solids, 154, p. 104532.

[35] Zhang, E., Spronck, B., Humphrey, J. D., and Karniadakis, G. E., 2022, “G2Φnet: Relating genotype and biomechanical phenotype of tissues with deep learning,” PLOS Computational Biology, 18(10), p. e1010660.

[36] You, H., Zhang, Q., Ross, C. J., Lee, C.-H., Hsu, M.-C., and Yu, Y., 2022, “A physics-guided neural operator learning approach to model biological tissues from digital image correlation measurements,” Journal of Biomechanical Engineering, 144(12), p. 121012.

[37] Flaschel, M., Kumar, S., and De Lorenzis, L., 2021, “Unsupervised discovery of interpretable hyperelastic constitutive laws,” Comput Method Appl M, 381, p. 113852.

[38] Thakolkaran, P., Joshi, A., Zheng, Y., Flaschel, M., De Lorenzis, L., and Kumar, S., 2022, “NN-EUCLID: Deep-learning hyperelasticity without stress data,” J Mech Phys Solids, 169, p. 105076.

[39] Flaschel, M., Kumar, S., and De Lorenzis, L., 2022, “Discovering plasticity models without stress data,” Npj Comput Mater, 8(1), p. 91.

[40] Marino, E., Flaschel, M., Kumar, S., and De Lorenzis, L., 2023, “Automated identification of linear viscoelastic constitutive laws with EUCLID,” Mechanics of Materials, 181, p. 104643.

[41] Gu, G. X., Chen, C. T., Richmond, D. J., and Buehler, M. J., 2018, “Bioinspired hierarchical composite design using machine learning: simulation, additive manufacturing, and experiment,” Mater Horiz, 5(5), pp. 939-945.

[42] Kumar, S., Tan, S. H., Zheng, L., and Kochmann, D. M., 2020, “Inverse-designed spinodoid metamaterials,” Npj Comput Mater, 6(1).

[43] Bastek, J. H., Kumar, S., Telgen, B., Glaesener, R. N., and Kochmann, D. M., 2022, “Inverting the structure-property map of truss metamaterials by deep learning,” P Natl Acad Sci USA, 119(1).

[44] Wu, L. L., Liu, L., Wang, Y., Zhai, Z. R., Zhuang, H. L., Krishnaraju, D., Wang, Q. X., and Jiang, H. Q., 2020, “A machine learning -based method to design modular metamaterials,” Extreme Mech Lett, 36.

[45] Wang, L. W., Chan, Y. C., Ahmed, F., Liu, Z., Zhu, P., and Chen, W., 2020, “Deep generative modeling for mechanistic-based learning and design of metamaterial systems,” Comput Method Appl M, 372.

[46] Cecen, A., Dai, H. J., Yabansu, Y. C., Kalidindi, S. R., and Song, L., 2018, “Material structure-property linkages using three-dimensional convolutional neural networks,” Acta Mater, 146, pp. 76-84.

[47] Deng, B. L., Zareei, A., Ding, X. X., Weaver, J. C., Rycroft, C. H., and Bertoldi, K., 2022, “Inverse Design of Mechanical Metamaterials with Target Nonlinear Response via a Neural Accelerated Evolution Strategy,” Adv Mater, 34(41).

[48] Guo, K., Yang, Z. Z., Yu, C. H., and Buehler, M. J., 2021, “Artificial intelligence and machine learning in design of mechanical materials,” Mater Horiz, 8(4), pp. 1153-1172.

[49] Butler, K. T., Davies, D. W., Cartwright, H., Isayev, O., and Walsh, A., 2018, “Machine learning for molecular and materials science,” Nature, 559(7715), pp. 547-555.

[50] Muhammad, Kennedy, J., and Lim, C. W., 2022, “Machine learning and deep learning in phononic crystals and metamaterials-A review,” Mater Today Commun, 33.

[51] Wang, Y. Z., Zeng, Q. L., Wang, J. Z., Li, Y., and Fang, D. N., 2022, “Inverse design of shell-based mechanical metamaterial with customized loading curves based on machine learning and genetic algorithm,” Comput Method Appl M, 401.

[52] Alderete, N. A., Pathak, N., and Espinosa, H. D., 2022, “Machine learning assisted design of shape-programmable 3D kirigami metamaterials,” Npj Comput Mater, 8(1).

[53] Alderete, N. A., Medina, L., Lamberti, L., Sciammarella, C., and Espinosa, H. D., 2021, “Programmable 3D structures via Kirigami engineering and controlled stretching,” Extreme Mech Lett, 43.

[54] Ma, C. P., Chang, Y. L., Wu, S., and Zhao, R. R., 2022, “Deep Learning-Accelerated Designs of Tunable Magneto-Mechanical Metamaterials,” Acs Appl Mater Inter, 14(29), pp. 33892-33902.

[55] Mao, Y. W., He, Q., and Zhao, X. H., 2020, “Designing complex architectured materials with generative adversarial networks,” Sci Adv, 6(17).

[56] Bessa, M. A., Glowacki, P., and Houlder, M., 2019, “Bayesian Machine Learning in Metamaterial Design: Fragile Becomes Supercompressible,” Adv Mater, 31(48).

[57] Jin, H., Zhang, E., Zhang, B., Krishnaswamy, S., Karniadakis, G. E., and Espinosa, H. D., 2023, “Mechanical Characterization and Inverse Design of Stochastic Architected Metamaterials Using Neural Operators,” arXiv preprint arXiv:2311.13812.

[58] Ngiam, J., Khosla, A., Kim, M., Nam, J., Lee, H., and Ng, A. Y., “Multimodal deep learning,” Proc. Proceedings of the 28th international conference on machine learning (ICML-11), pp. 689-696.

[59] Meng, X. H., and Karniadakis, G. E., 2020, “A composite neural network that learns from multi-fidelity data: Application to function approximation and inverse PDE problems,” J Comput Phys, 401.

[60] Trask, N., Martinez, C., Lee, K., and Boyce, B., 2022, “Unsupervised physics-informed disentanglement of multimodal data for high-throughput scientific discovery,” arXiv preprint arXiv:2202.03242.

[61] Lu, L., Dao, M., Kumar, P., Ramamurty, U., Karniadakis, G. E., and Suresh, S., 2020, “Extraction of mechanical properties of materials through deep learning from instrumented indentation,” P Natl Acad Sci USA, 117(13), pp. 7052-7062.

[62] Smith, R. C., 2013, Uncertainty quantification: theory, implementation, and applications, Siam.

[63] Abdar, M., Pourpanah, F., Hussain, S., Rezazadegan, D., Liu, L., Ghavamzadeh, M., Fieguth, P., Cao, X., Khosravi, A., and Acharya, U. R., 2021, “A review of uncertainty quantification in deep learning: Techniques, applications and challenges,” Information Fusion, 76, pp. 243-297.

[64] Soize, C., 2017, Uncertainty quantification, Springer.

[65] Sullivan, T. J., 2015, Introduction to uncertainty quantification, Springer.

[66] Bayes, T., 1763, “LII. An essay towards solving a problem in the doctrine of chances. By the late Rev. Mr. Bayes, FRS communicated by Mr. Price, in a letter to John Canton, AMFR S,” Philosophical transactions of the Royal Society of London(53), pp. 370-418.

[67] Cicci, L., Fresca, S., Guo, M., Manzoni, A., and Zunino, P., 2023, “Uncertainty quantification for nonlinear solid mechanics using reduced order models with Gaussian process regression,” arXiv preprint arXiv:2302.08216.

[68] Liang, M., Chang, Z., Wan, Z., Gan, Y., Schlangen, E., and Šavija, B., 2022, “Interpretable Ensemble-Machine-Learning models for predicting creep behavior of concrete,” Cement and Concrete Composites, 125, p. 104295.

[69] Zhang, Y. P., Hart, J. D., and Needleman, A., 2019, “Identification of Plastic Properties From Conical Indentation Using a Bayesian-Type Statistical Approach,” J Appl Mech-T Asme, 86(1).

[70] de Oca Zapiain, D. M., Lim, H., Park, T., and Pourboghrat, F., 2022, “Predicting plastic anisotropy using crystal plasticity and Bayesian neural network surrogate models,” Materials Science and Engineering: A, 833, p. 142472.

[71] Pyrialakos, S., Kalogeris, I., Sotiropoulos, G., and Papadopoulos, V., 2021, “A neural network-aided Bayesian identification framework for multiscale modeling of nanocomposites,” Comput Method Appl M, 384, p. 113937.

[72] Ravindran, S., Gandhi, V., Joshi, A., and Ravichandran, G., 2022, “Three dimensional full-field velocity measurements in shock compression experiments using stereo digital image correlation,” arXiv preprint arXiv:2210.12568.

[73] Saccone, M. A., Gallivan, R. A., Narita, K., Yee, D. W., and Greer, J. R., 2022, “Additive manufacturing of micro-architected metals via hydrogel infusion,” Nature, pp. 1-2.

[74] Li, Y., Jin, H., Zhou, W., Wang, Z., Lin, Z., Mirkin, C. A., and Espinosa, H. D., 2023, “Ultrastrong colloidal crystal metamaterials engineered with DNA,” Sci Adv, 9(39), p. eadj8103.

[75] Jin, H., and Espinosa, H. D., 2023, “Mechanical Metamaterials Fabricated from Self-assembly: A Perspective,” Journal of Applied Mechanics, pp. 1-25.