The central component of the improved ML algorithm is the geometric inductive bias built into our feature mapping \(x\in {[-1,1]}^{m}\mapsto \phi (x)\in {{\mathbb{R}}}^{{m}_{\phi }}\). To describe the ML algorithm, we first need to present some definitions relating to this geometric structure.

Definitions of the geometric inductive bias

We consider n qubits arranged at locations, or sites, in a d-dimensional space, e.g., a spin chain (d = 1), a square lattice (d = 2), or a cubic lattice (d = 3). This geometry is characterized by the distance \({d}_{{{{{{{{\rm{qubit}}}}}}}}}(i,{i}^{{\prime} })\) between any two qubits i and \({i}^{{\prime} }\). Using the distance d_qubit between qubits, we can define the geometry of local observables. Given any two observables O_A, O_B on the n-qubit system, we define the distance d_obs(O_A, O_B) between the two observables as the minimum distance between the qubits that O_A and O_B act on. We also say an observable is geometrically local if it acts nontrivially only on nearby qubits under the distance metric d_qubit. We then define S^(geo) as the set of all geometrically local Pauli observables, i.e., geometrically local observables that belong to the set {I, X, Y, Z}^⊗n. The size of S^(geo) is \({{{{{{{\mathcal{O}}}}}}}}(n)\), linear in the total number of qubits.

With these basic definitions in place, we now define a few more geometric objects. The first object is the set of coordinates in the m-dimensional vector x that are close to a geometrically local Pauli observable P. This is formally given by,

where h_j(c) is the few-body interaction term in the n-qubit Hamiltonian H(x) whose parameters \({\overrightarrow{x}}_{j(c)}\) include the variable x_c ∈ [ − 1, 1], and δ₁ is an efficiently computable hyperparameter that is determined later. Each variable x_c in the m-dimensional vector x corresponds to exactly one interaction terms \({h}_{j(c)}={h}_{j(c)}({\overrightarrow{x}}_{j(c)})\), where the parameter vector \({\overrightarrow{x}}_{j(c)}\) contains the variable x_c. Intuitively, I_P is the set of coordinates that have the strongest influence on the function \({{{{{{{\rm{Tr}}}}}}}}(P\rho (x))\).

The second geometric object is a discrete lattice over the space [−1, 1]^m associated to each subset I_P of coordinates. For any geometrically local Pauli observable P ∈ S^(geo), we define X_P to contain all vectors x that take on value 0 for coordinates outside I_P and take on a set of discrete values for coordinates inside I_P. Formally, this is given by

where δ₂ is an efficiently computable hyperparameter to be determined later. The definition of X_P is meant to enumerate all sufficiently different vectors for coordinates in the subset I_P ⊆ {1, …, m}.

Now given a geometrically local Pauli observable P and a vector x in the discrete lattice X_P ⊆ [−1, 1]^m, the third object is a set T_x,P of vectors in [−1, 1]^m that are close to x for coordinates in I_P. This is formally defined as,

The set T_x,P is defined as a thickened affine subspace close to the vector x for coordinates in I_P. If a vector \({x}^{{\prime} }\) is in T_x,P, then \({x}^{{\prime} }\) is close to x for all coordinates in I_P, but \({x}^{{\prime} }\) may be far away from x for coordinates outside of I_P. Examples of these definitions are given in Supplementary Figs. 1 and 2.

Feature mapping and ML model

We can now define the feature map ϕ taking an m-dimensional vector x to an m_ϕ-dimensional vector ϕ(x) using the thickened affine subspaces \({T}_{{x}^{{\prime} },P}\) for every geometrically local Pauli observable P ∈ S^(geo) and every vector \({x}^{{\prime} }\) in the discrete lattice X_P. The dimension of the vector ϕ(x) is given by \({m}_{\phi }={\sum }_{P\in {S}^{{{{{{{{\rm{(geo)}}}}}}}}}}| {X}_{P}|\). Each coordinate of the vector ϕ(x) is indexed by \({x}^{{\prime} }\in {X}_{P}\) and P ∈ S^(geo) with

which is the indicator function checking if x belongs to the thickened affine subspace. Recall that this means each coordinate of the m_ϕ-dimensional vector ϕ(x) checks if x is close to a point \({x}^{{\prime} }\) on a discrete lattice X_P for the subset I_P of coordinates close to a geometrically local Pauli observable P.

The classical ML model we consider is an ℓ₁-regularized regression (LASSO) over the ϕ(x) space. More precisely, given an efficiently computable hyperparameter B > 0, the classical ML model finds an m_ϕ-dimensional vector w^* from the following optimization problem,

where \({\{({x}_{\ell },{y}_{\ell })\}}_{\ell=1}^{N}\) is the training data. Here, x_ℓ ∈ [−1, 1]^m is an m-dimensional vector that parameterizes a Hamiltonian H(x) and y_ℓ approximates \({{{{{{{\rm{Tr}}}}}}}}(O\rho ({x}_{\ell }))\). The learned function is given by h^*(x) = w^* ⋅ ϕ(x). The optimization does not have to be solved exactly. We only need to find a w^* whose function value is \({{{{{{{\mathcal{O}}}}}}}}(\epsilon )\) larger than the minimum function value. There is an extensive literature^{53,54,55,56,57,58,59} improving the computational time for the above optimization problem. The best known classical algorithm⁵⁸ has a computational time scaling linearly in m_ϕ/ϵ² up to a log factor, while the best known quantum algorithm⁵⁹ has a computational time scaling linearly in \(\sqrt{{m}_{\phi }}/{\epsilon }^{2}\) up to a log factor.

Rigorous guarantee

The classical ML algorithm given above yields the following sample and computational complexity. This theorem improves substantially upon the result in³⁶, which requires \(N={n}^{{{{{{{{\mathcal{O}}}}}}}}(1/\epsilon )}\). The proof idea is given in Section “Methods”, and the detailed proof is given in Supplementary Sections 1, 2, 3. Using the proof techniques presented in this work, one can show that the sample complexity \(N=\log (n/\delta ){2}^{{{{{{{{\rm{polylog}}}}}}}}(1/\epsilon )}\) also applies to any sum of few-body observables O = ∑_jO_j with ∑_j∥O_j∥_∞≤1, even if the operators {O_j} are not geometrically local.

Theorem 1

(Sample and computational complexity). Given \(n,\,\delta \, > \, 0,\,\frac{1}{e} \, > \,\epsilon \, > \, 0\) and a training data set \({\{{x}_{\ell },{y}_{\ell }\}}_{\ell=1}^{N}\) of size

where x_ℓ is sampled from an unknown distribution \({{{{{{{\mathcal{D}}}}}}}}\) and \(| {y}_{\ell }-{{{{{{{\rm{Tr}}}}}}}}(O\rho ({x}_{\ell }))| \le \epsilon\) for any observable O with eigenvalues between −1 and 1 that can be written as a sum of geometrically local observables. With a proper choice of the efficiently computable hyperparameters δ₁, δ₂, and B, the learned function h^*(x) = w^* ⋅ ϕ(x) satisfies

with probability at least 1 − δ. The training and prediction time of the classical ML model are bounded by \({{{{{{{\mathcal{O}}}}}}}}(nN)=n\log (n/\delta ){2}^{{{{{{{{\rm{polylog}}}}}}}}(1/\epsilon )}\).

The output y_ℓ in the training data can be obtained by measuring \({{{{{{{\rm{Tr}}}}}}}}(O\rho ({x}_{\ell }))\) for the same observable O multiple times and averaging the outcomes. Alternatively, we can use the classical shadow formalism^{48,49,50,51,52,60} that performs randomized Pauli measurements on ρ(x_ℓ) to predict \({{{{{{{\rm{Tr}}}}}}}}(O\rho ({x}_{\ell }))\) for a wide range of observables O. We can also combine Theorem 1 and the classical shadow formalism to use our ML algorithm to predict ground state representations, as seen in the following corollary. This allows one to predict ground state properties \({{{{{{{\rm{Tr}}}}}}}}(O\rho (x))\) for a large number of observables O rather than just a single one. We present the proof of Corollary 1 in Supplementary Section 3B.

Corollary 1

Given \(n,\,\delta\, > \, 0,\,\frac{1}{e} \, > \, \epsilon \, > \, 0\) and a training data set \({\{{x}_{\ell },{\sigma }_{T}(\rho ({x}_{\ell }))\}}_{\ell=1}^{N}\) of size

where x_ℓ is sampled from an unknown distribution \({{{{{{{\mathcal{D}}}}}}}}\) and σ_T(ρ(x_ℓ)) is the classical shadow representation of the ground state ρ(x_ℓ) using T randomized Pauli measurements. For \(T=\tilde{{{{{{{{\mathcal{O}}}}}}}}}(\log (n)/{\epsilon }^{2})\), then the proposed ML algorithm can learn a ground state representation \({\hat{\rho }}_{N,T}(x)\) that achieves

for any observable O with eigenvalues between −1 and 1 that can be written as a sum of geometrically local observables with probability at least 1 − δ.

We can also show that the problem of estimating ground state properties for the class of parameterized Hamiltonians \(H(x)={\sum }_{j}{h}_{j}({\overrightarrow{x}}_{j})\) considered in this work is hard for non-ML algorithms that cannot learn from data, assuming the widely believed conjecture that NP-complete problems cannot be solved in randomized polynomial time. This is a manifestation of the computational power of data studied in⁶¹. The proof of Proposition 1 in³⁶ constructs a parameterized Hamiltonian H(x) that belongs to the family of parameterized Hamiltonians considered in this work and hence establishes the following.

Proposition 1

(A variant of Proposition 1 in³⁶). Consider a randomized polynomial-time classical algorithm \({{{{{{{\mathcal{A}}}}}}}}\) that does not learn from data. Suppose for any smooth family of gapped 2D Hamiltonians \(H(x)={\sum }_{j}{h}_{j}({\overrightarrow{x}}_{j})\) and any single-qubit observable \(O,{{{{{{{\mathcal{A}}}}}}}}\) can compute ground state properties \({{{{{{{\rm{Tr}}}}}}}}(O\rho (x))\) up to a constant error averaged over x ∈ [−1, 1]^m uniformly. Then, NP-complete problems can be solved in randomized polynomial time.

This proposition states that even under the restricted settings of considering only 2D Hamiltonians and single-qubit observables, predicting ground state properties is a hard problem for non-ML algorithms. When one consider higher-dimensional Hamiltonians and multi-qubit observables, the problem only becomes harder because one can embed low-dimensional Hamiltonians in higher-dimensional spaces.

Numerical experiments

We present numerical experiments to assess the performance of the classical ML algorithm in practice. The results illustrate the improvement of the algorithm presented in this work compared to those considered in³⁶, the mild dependence of the sample complexity on the system size n, and the inherent geometry exploited by the ML models. We consider the classical ML models previously described, utilizing a random Fourier feature map⁶². While the indicator function feature map was a useful tool to obtain our rigorous guarantees, random Fourier features are more robust and commonly used in practice. Moreover, we still expect our rigorous guarantees to hold with this change because Fourier features can approximate any function, which is the central property of the indicator functions used in our proofs. Furthermore, we determine the optimal hyperparameters using cross-validation to minimize the root-mean-square error (RMSE) and then evaluate the performance of the chosen ML model using a test set. The models and hyperparameters are further detailed in Supplementary Section 4.

For these experiments, we consider the two-dimensional antiferromagnetic random Heisenberg model consisting of 4 × 5 = 20 to 9 × 5 = 45 spins as considered in previous work³⁶. In this setting, the spins are placed on sites in a 2D lattice. The Hamiltonian is

where the summation ranges over all pairs 〈ij〉 of neighboring sites on the lattice and the couplings {J_ij} are sampled uniformly from the interval [0, 2]. Here, the vector x is a list of all couplings J_ij so that the dimension of the parameter space is m = O(n), where n is the system size. The nonnegative interval [0, 2] corresponds to antiferromagnetic interactions. To minimize the Heisenberg interaction terms, nearby qubits have to form singlet states. While the square lattice is bipartite and lacks the standard geometric frustration, the presence of disorder makes the ground state calculation more challenging as neighboring qubits will compete in the formation of singlets due to the monogamy of entanglement⁶³.

We trained a classical ML model using randomly chosen values of the parameter vector x = {J_ij}. For each parameter vector of random couplings sampled uniformly from [0, 2], we approximated the ground state using the same method as in³⁶, namely with the density-matrix renormalization group (DMRG)⁶⁴ based on matrix product states (MPS)⁶⁵. The classical ML model was trained on a data set \({\{{x}_{\ell },{\sigma }_{T}(\rho ({x}_{\ell }))\}}_{\ell=1}^{N}\) with N randomly chosen vectors x, where each x corresponds to a classical representation σ_T(ρ(x_ℓ)) created from T randomized Pauli measurements⁴⁸. For a given training set size N, we conduct 4-fold cross validation on the N data points to select the best hyperparameters, train a model with the best hyperparameters on the N data points, and test the performance on a test set of size N. Further details are discussed in Supplementary Section 4.

The ML algorithm predicted the classical representation of the ground state for a new vector x. These predicted classical representations were used to estimate two-body correlation functions, i.e., the expectation value of

for each pair of qubits 〈ij〉 on the lattice. Here, we are using the combination of our ML algorithm with the classical shadow formalism as described in Corollary 1, leveraging this more powerful technique to predict a large number of ground state properties.

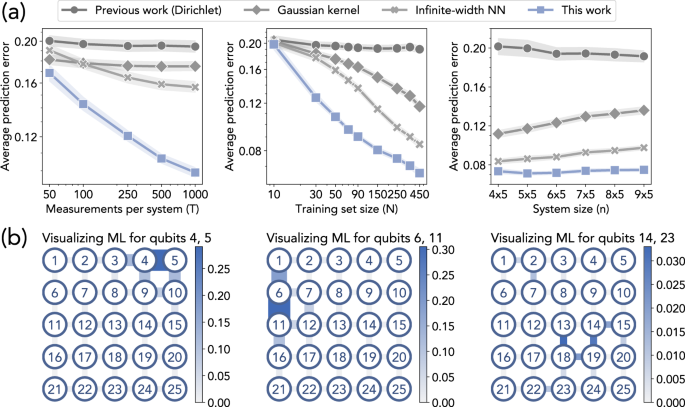
In Fig. 2A, we can clearly see that the ML algorithm proposed in this work consistently outperforms the ML models implemented in³⁶, which includes the rigorous polynomial-time learning algorithm based on Dirichlet kernel proposed in³⁶, Gaussian kernel regression^66,67, and infinite-width neural networks^68,69. Figure 2A (Left) and (Center) show that as the number T of measurements per data point or the training set size N increases, the prediction performance of the proposed ML algorithm improves faster than the other ML algorithms. This observation reflects the improvement in the sample complexity dependence on prediction error ϵ. The sample complexity in³⁶ depends exponentially on 1/ϵ, but Theorem 1 establishes a quasi-polynomial dependence on 1/ϵ. From Fig. 2A (Right), we can see that the ML algorithms do not yield a substantially worse prediction error as the system size n increases. This observation matches with the \(\log (n)\) sample complexity in Theorem 1, but not with the poly(n) sample complexity proven in³⁶. These improvements are also relevant when comparing the ML predictions to actual correlation function values. Figure 3 in³⁶ illustrates that for the average prediction error achieved in their work, the predictions by the ML algorithm match the simulated values closely. In this work, we emphasize that significantly less training data is needed to achieve the same prediction error³⁶ and agree with the simulated values.

a Prediction error. Each point indicates the root-mean-square error for predicting the correlation function in the ground state (averaged over Heisenberg model instances and each pair of neighboring spins). We present log-log plots for the scaling of prediction error ϵ with T and N: the slope corresponds to the exponent of the polynomial function ϵ(T), ϵ(N). The shaded regions show the standard deviation over different spin pairs. b Visualization. We plot how much each coupling J_ij contributes to the prediction of the correlation function over different pairs of qubits in the trained ML model. Thicker and darker edges correspond to higher contributions. We see that the ML model learns to utilize the local geometric structure.

An important step for establishing the improved sample complexity in Theorem 1 is that a property on a local region R of the quantum system only depends on parameters in the neighborhood of region R. In Fig. 2B, we visualize where the trained ML model is focusing on when predicting the correlation function over a pair of qubits. A thicker and darker edge is considered to be more important by the trained ML model. Each edge of the 2D lattice corresponds to a coupling J_ij. For each edge, we sum the absolute values of the coefficients in the ML model that correspond to a feature that depends on the coupling J_ij. We can see that the ML model learns to focus only on the neighborhood of a local region R when predicting the ground state property.